Разработка элективного курса по теме: «Кривые второго порядка»

уравнение директрисы D2:

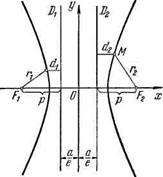
Рис. 15

Директрисы гиперболы целиком расположены в области G, не содержащей точек. В самом деле, ранее мы убедились, что полоса G1 определяемая в выбранной системе координат Оху неравенством |х|<а, содержится в области G. Но эта полоса содержит директрисы гиперболы, так как, согласно (1.31), для точек директрис |x| =, либо для гиперболы е>1. Расположение директрис гиперболы указано на рис. 6.11.Следовательно, мы можем обосновать расположение директрис гиперболы, указанное на рис. 6.11. Очевидно, что точки левой (правой) ветви гиперболы и ее центр О расположены по разные стороны от директрисы D1 (D2), а точки правой (левой) ветви гиперболы и ее центр О расположены по одну сторону от директрисы D1 (D2).

Обозначим через р расстояние от фокуса гиперболы до соответствующей этому фокусу директрисы. Поскольку расстояние от центра гиперболы до директрисы равно а расстояние от центра гиперболы до фокуса равно с, то . Так как с=ае, то для р получаем формулу

(1.32)

Докажем теорему, выясняющую важное свойство гиперболы и ее директрис.

Теорема 1.2. Отношение расстояния r1 от точки М гиперболы до фокуса Fi к расстоянию di от этой точки до отвечающей этому фокусу директрисы Di равно эксцентриситету е этой гиперболы.

Доказательство. Для доказательства этой теоремы нужно рассмотреть следующие четыре случая: 1) точка M находится на левой ветви гиперболы, исследуется фокус F1 и директриса D1, 2) точка М находится на правой ветви гиперболы, исследуется фокус F1 и директриса D1; 3) точка М на левой ветви, фокус F2, директриса D2; 4) точка М на правой ветви, фокус F2, директриса D2. Так как рассуждения для каждого из случаев однотипны, то мы ограничимся лишь первым случаем. Начало декартовой прямоугольной системы координат в середине отрезка FiF2, а оси Ох и Оу направим так, как указано на рис. 6.11. Так как абсцисса х любой точки М(х, у) левой ветви гиперболы отрицательна, то расстояние r1 от этой точки до фокуса F1 согласно формулам (1.11), равно . Так как , то для r1 получим выражение

r1=(1.33)

Директриса D1 определяется первым из уравнений (1.31). Нормированное уравнение этой директрисы имеет вид

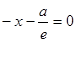(1.34)

Так как точка М левой ветви гиперболы и начало координат находятся по разные стороны от директрисы DI,, то расстояние d1 от точки М до директрисы D1 равно отклонению М от D1 и мы получим (в силу (1.34) и теоремы 1.1):

.(1.35)

Используя формулы (1.33) и (1.35), найдем, . Для первого случая теорема доказана. Остальные случаи рассматриваются аналогично.

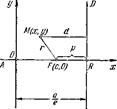
Рис. 16

Определение эллипса и гиперболы, основанное на их свойстве по отношению к директрисам.

Теоремы 1.1 и 1.2, доказанные в предыдущем пункте, выясняют свойство отличного от окружности эллипса и гиперболы, связанное с директрисами этих кривых. Убедимся в том, что это свойство эллипса и гиперболы может быть принято в качестве их определения. Рассмотрим в плоскости точку F и прямую D (рис. 6.12). Будем предполагать, что точка F не лежит на прямой D. Докажем следующее утверждение.

Теорема 1.3. Геометрическое место точек М плоскости , для которых отношение е расстояния r до точки F к расстоянию d до прямой D есть величина постоянная, представляет собой эллипс (при е<1) или гиперболу (при е>1). При этом точка F называется фокусом, а прямая D - директрисой рассматриваемого геометрического места.

Другая информация:

Элективные курсы в образовательной области «Математика»
Среди школьных предметов математика занимает совершенно особое место. В середине прошлого века в старших классах отечественной школы много внимания и как следствие учебного времени уделялось математике. Специфика преподавания математики в старших классах во многом определяется тем, что экзамен по м ...

Исследование чувства гражданственности у детей
Изучив психолого-педагогическую и методическую литературу, мы решили провести опытно-экспериментальную работу по данной проблеме. Исследование проводилось в МБДОУ "Детский сад № 19" Нижнекамского муниципального района Республики Татарстан. Экспериментальная группа состоит из детей дошколь ...

Обобщение результатов констатирующего исследования
При проведении логопедического обследования мы учитывали тот факт, что дети никогда ранее не занимались с логопедом и некоторые ситуации были для них незнакомыми, новыми. Дети терялись, зажимались, хоть и не отказывались от выполнения заданий - было видно, что они волнуются. Учет данного факта проя ...