Разработка элективного курса по теме: «Кривые второго порядка»

10. Касательные к эллипсу, гиперболе и параболе

1. Уравнения касательных к эллипсу, гиперболе и параболе. Убедимся, что каждая из кривых L, являющаяся эллипсом, гиперболой или параболой, представляет собой объединение графиков двух функций. Рассмотрим, например, каноническое уравнение эллипса. Из этого уравнения следует, Что часть эллипса, точки которой имеют неотрицательные ординаты у, есть график функции.математический обучение элективный эллипс гипербола

(1.51)

а часть эллипса, точки которой имеют неположительные ординаты, есть график функции

. (1.52)

Обращаясь к каноническому уравнению гиперболы (1.9), найдем, что гипербола представляет собой объединение графиков функций

и , при xa и x-a (1.53)

а из канонического уравнения параболы (1.15) вытекает, что эта кривая есть объединение графиков функций

и при (1.54)

Рассмотрим теперь вопрос о касательных к эллипсу, гиперболе и параболе. Естественно, что касательные к этим кривым, будут также касательными к графикам функций (1.51) -(1.54) Найдем, уравнение касательной к эллипсу в его точке М(х, у), считая при этом у0 (пусть, у>0). Пусть X, Y - текущие координаты точки касательной. Так как ее угловойкоэффициент k=y’ где у'=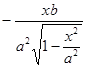

производная функции (1,51), вычисленная в точке х, то уравнение касательной имеет вид

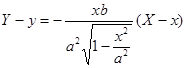
Учитывая, что точка М(х, у) лежит на эллипсе (т. е ее координаты х и у удовлетворяют уравнениям (1.51) и (1.4)), получим, после несложных преобразований, уравнение касательной к эллипсу в следующей форме-

для эллипса (1.56)

Рассуждая аналогично для случая гиперболы и параболы, получим следующие уравнения касательных к этим кривым:

для гиперболы

для параболы В предыдущих рассуждениях был исключен случай y=0. В соответствующих точках эллипса, гиперболы и параболы касательные вертикальны. Легко убедиться, что уравнения (1.56) - (1.58) справедливы и в этом случае. Отметим, что касательная к эллипсу имеет с ним только одну общую точку - точку касания Аналогичным свойством обладают касательные к гиперболе и параболе.

11. Фокальные свойства

Оптические свойства эллипса, гиперболы и параболы. Установим следующее оптическое свойство эллипса: лучи света, исходящие из одного фокуса F1 эллипса после зеркального отражения от эллипса проходят через второй фокус F2 (рис. 17). Геометрически указанное свойство означает, что отрезки MF1 и MF2 образуют с касательной в точке М эллипса равные углы.

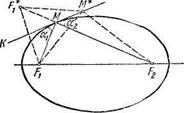
Рис. 17

Допустим, что эллипс не обладает указанным свойством, т. е (рис. 17). Пусть F*1- зеркальное отражение фокуса F, относительно касательной К в точке М. Соединим F*1, с М и F2 Так как , то точка М* пересечения прямой F*1 F2 с касательной К не совпадает с точкой М Поэтому |F1 M*| +|F2M*| =| F*1F2| < |F1 M| +|F2 M|=2a.(1.59)

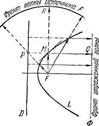
Рис. 18

Будем теперь перемещать точку М* по касательной К от точки М. При таком перемещении сyмма |F1M*|+|F2M*| неограниченно увеличивается. В начальный момент перемещения эта сумма, согласно (1.59), была меньше 2а. Поэтому в некоторый момент эта сумма будет равна 2а, а это означает, что на касательной K, кроме точки М, будет еще одна точка М* эллипса, отличная от М, но этого не может быть. Таким образом, указанное выше свойство эллипса действительно справедливо.

Другая информация:

Выявление уровня сформированности экологических знаний у старших дошкольников
В предыдущей главе были рассмотрены теории воспитания экологической культуры у детей дошкольного возраста в целом и через игровую деятельность. Экологическая культура имеет отчётливые внешние проявления, а именно: ценностное отношение к природе, к себе и к другим людям как части природы, к вещам и ...

Воспитание патриотизма как основа воспитания чувства гражданственности у детей дошкольного возраста
Чрезвычайно важным в проблемы воспитания чувств гражданственности является общепринятое мнение о том, что этот процесс необходимо начинать в дошкольном возрасте. В этот период происходит формирование духовно-нравственной основы ребенка, эмоций, чувств, мышления, механизмов социальной адаптации в об ...

Чистые продукты питания и здоровье человека
Каждый человек знает, что пища необходима для нормальной жизнедеятельности организма. Но мы часто употребляем в пищу то, что вкусно, что можно быстро приготовить, и не очень задумываемся о полезности и доброкачественности употребляемых продуктов. Врачи утверждают, что полноценное рациональное питан ...