Разработка элективного курса по теме: «Кривые второго порядка»

Выберем начало декартовой прямоугольной системы координат в середине отрезка F1F2. а оси Ох и Оу направим так, как указано на рис. 6.10. Тогда, очевидно, уравнения директрис Di (i=1,2) эллипс можно записать следующим образом:

уравнение директрисы D1: x = -

уравнение директрисы D2: х =

Директрисы эллипса расположены вне эллипса. Действительно, эллипс расположен в прямоугольнике |х|а, |у|b стороны которого перпендикулярны большой и малой осям эллипса.

Из определения директрис вытекает, что они параллельны двум перпендикулярным большой оси эллипса сторонам этого прямоугольника. Поскольку упомянутые стороны отстоят от центра эллипса на расстоянии а, а директрисы - на расстоянии >а (0<е<1), то директрисы расположены вне прямоугольника, а следовательно, и вне эллипса.

Как мы только что выяснили, директрисы расположены вне эллипса. Отсюда вытекает, что точки эллипса и его центр расположены по одну сторону от каждой из его директрис.

Обозначим через р расстояние от фокуса эллипса до соответствующей этому фокусу директрисы. Поскольку расстояние от центра эллипса до директрисы равно а расстояние от центра эллипса до фокуса равно с, то р равно -с. Так как с = ае, то для р получаем следующее выражение

(1.27)

Докажем теорему, выясняющую важное свойство отличного от окружности эллипса и его директрис.

Теорема 1.1. Отношение расстояния ri от точки М эллипса до фокуса Fi к расстоянию di от этой точки до отвечающей этому фокусу директрисы Di равно эксцентриситету е этого эллипса.

Доказательство. Пусть F1 и F2 - фокусы эллипса. Выберем декартову прямоугольную систему координат см. рис. 6.10. выше мы выяснили, что при таком выборе системы координат расстояния r1 и r2 от точки М(х,у) эллипса до фокусов F1 и F2 определяются формулами (1.6). Так как отношение -

равно эксцентриситету е этого эллипса, то для r1 и г2 мы получим выражения

r1 = a+ex, r2=а- ex.(1.28)

Найдем теперь расстояния di от точки М эллипса до директрис Di. Используя уравнения директрис Di (см. формулы (1.26)), легко убедиться в том, что нормированные уравнения директрис имеют вид

D1:= 0 D2: = 0 (1.29)

Так как точка М(х, у) эллипса и начало координат находятся по одну сторону от каждой из директрис, то расстояния d1 и d2 от точки М(х, y) до директрис D1 и D2 равны соответствующим отклонениям М(х, у) от D1 и D2, взятым со знаком минус, и мы получим (в силу (1.29)):

(1.30)

Используя формулы (1.28) и (1.30), найдем, что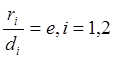

Теорема доказана.

Директрисы гиперболы. Обозначим через с половину расстояния между фокусами F1 и F2 гиперболы, через а ее действительную полуось и через О ее центр (рис. 6.11). Пусть е - эксцентриситет этой гиперболы и - плоскость, в которой расположена гипербола. Мнимая ось гиперболы разбивает эту плоскость на две полуплоскости. Обозначим через i, (i=1,2) ту из этих полуплоскостей, в которой лежит фокус Fi (i=1,2).

Определение. Директрисой Di (i=1,2) гиперболы, отвечающей фокусу Fi (i=1,2), называется прямая, расположенная в полуплоскости i (i=1,2) перпендикулярно действительной оси гиперболы на расстоянии - от ее центра.

Выберем начало декартовой прямоугольной системы координат в середине отрезка FiF2, а оси Ох и Оу направим так, как указано на рис. 6.11. Тогда, очевидно, уравнения директрис Di (i=1,2) гиперболы можно записать следующим образом:

уравнение директрисы Di:

Другая информация:

Новый взгляд христианства на человеческую личность
Прежде всего, Христианство принесло с собой новый взгляд на человеческую личность. В античном мире человек расценивался, если не исключительно, то преимущественно, — особенно в те первые времена, — с точки зрения полезности его для государства, для общества. Человек здесь имел свою цену, прежде все ...

Особенности распознавания семантически далеких значений
Следующая группа заданий была направлена на исследование распознавания семантически далеких значений. С заданиями данной группы большинство детей как экспериментальной, так и контрольной группы справились хорошо за исключением группы слов «трамвай, метро, дворник». Затруднения вызывало то, что мног ...

Планирование межпредметных связей
Содержание, объем, время и способы использования знаний из других предметов можно определить только на основе планирования. Для этого необходимо тщательное изучение рекомендаций, данных учебными программами в разделах «Межпредметные связи» по каждой учебной теме курса, а также изучение учебных план ...