Разработка элективного курса по теме: «Кривые второго порядка»

7. Парабола.

Рис. 10

Парабола

Определение. Параболой называется геометрическое место точек плоскости, для которых расстояние до некоторой фиксированной точки F этой плоскости равно расстоянию до некоторой фиксированной прямой, также расположенной в рассматриваемой плоскости.

Указанная в определении точка F называется фокусом параболы, а фиксированная прямая - директрисой параболы (Слово директриса означает направляющая).

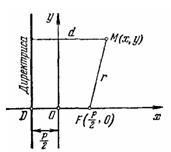
Рис. 11

Для вывода канонического уравнения параболы выберем начало О декартовой системы координат в середине отрезка FD, представляющего собой перпендикуляр, опущенный из фокуса F на директрису (при этом фокус F не лежит на директрисе, ибо в противном случае точки плоскости, для которых были бы выполнены условия определения параболы, располагались на прямой, проходящей через F перпендикулярно директрисе, т. е. парабола выродилась бы в прямую.), а оси Ох и Оу направим так, как указано на рис.6.3.

Пусть длина отрезка FD равна р. Тогда в выбранной системе координат точка F имеет координаты (,0)Пусть М - точка плоскости с координатами (х, у). Обозначим через r расстояние от М до F, а через d - расстояние от М до директрисы (рис. 6.3). Согласно определению параболы равенство r=d(1.12) является необходимым и достаточным условием расположения точки М на-данной параболе. Так как

(1.13)

то, согласно (1.12), соотношение представляет собой необходимое и достаточное условие расположения точки М с координатами х и у на данной параболе. Поэтому соотношение (1.14) можно рассматривать как уравнение параболы. Путем стандартного приема «уничтожения радикалов» это уравнение приводится к виду

у2 = 2рх. (1.15)

Убедимся в том, что уравнение (1.15), полученное путем алгебраических преобразований уравнения (1.14), не приобрело новых корней. Для этого достаточно доказать, что для каждой точки М, координаты x и y которой удовлетворяют уравнению (1.15), величины r и d равны (выполнено соотношение (1.12)).

Из соотношения (1.15) вытекает, что абсциссы х рассматриваемых точек неотрицательны,

т.е. х 0. Для точек с неотрицательными абсциссами . Найдем теперь выражение для расстояния r от точки М до F. Подставляя у из выражения (1.15) в правую часть выражения для r (1.13) и учитывая, что х 0, найдем, что . Таким образом, для рассматриваемых точек r=d, т. е. они располагаются на параболе.

Уравнение (1.15) называется каноническим уравнением параболы. Величина р называется параметром параболы.

Свойства параболы

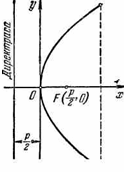
Рис. 12

1°. Парабола имеет только одну ось симметрии (ось параболы), в отличии от эллипса и гиперболы. Точка пересечения параболы с осью называется вершиной параболы. Действительно, в уравнении (1.15) величина у фигурирует в четной степени. Следовательно, если координаты х и у точки М удовлетворяют уравнению (1.15) (т. е. точка М располагается на параболе), то этому уравнению удовлетворяют координаты (х,-у) симметричной ей точки относительно оси Ох (рис. 6.8). Таким образом, если парабола задана своим каноническим уравнением (1.15), то осью этой параболы является ось Ох. Очевидно, вершиной параболы является начало координат.

2°. Вся парабола расположена в правой полуплоскости плоскости Оху. В самом деле, так как р>0, то уравнению (1.15) удовлетворяют координаты точек лишь с неотрицательными абсциссами. Такие точки располагаются в правой полуплоскости.

3°. Из рассуждений вытекает, что директриса параболы, определяемой каноническим уравнением (1.15), имеет уравнение (1.23)

4°. Любые две параболы подобны друг другу. Пусть у2 = 2рх и у2=2р*х - канонические уравнения этих парабол в декартовой системе Оху, y=kx - уравнение произвольной прямой, проходящей через О, а (х, у) и (х*,у*) - координаты точек пересечения этой прямой с параболами. Используя канонические уравнения, получим

Другая информация:

Умственная отсталость как форма нарушения интеллекта:классификация, виды и причины формирования
Понятие «умственная отсталость» (олигофрения) в отечественной специальной психологии понимается как стойкое нарушение познавательной деятельности, возникшее вследствие органического поражения головного мозга (наследуемого или приобретённого). Согласно современным научным представлениям, понятие «ум ...

Компонентный состав Триз
Теория решения изобретательских задач в образовательном процессе представлена в качестве внедрения основных её понятий. При этом ознакомить учащихся со всеми основами ТРИЗ за один урок невозможно, поскольку они требуют тщательного разбора и осознания. В основном, знакомство начинается с изобретател ...

Развитие диалогической речи у детей в детском саду
Программа детского сада предусматривает обучение диалогической речи. Работа по развитию диалогической речи направлена на формирование умений, необходимых для общения. Диалог — сложная форма социального взаимодействия. Участвовать в диалоге иногда бывает труднее, чем строить монологическое высказыва ...