Разработка элективного курса по теме: «Кривые второго порядка»

r1= - а - , при х<0

- а+, при x>0

r2=

а - , при х<0 (1.11)

Таким образом, для рассматриваемой точки М имеем |r1-r2| =2а, и поэтому она располагается на гиперболе.

Уравнение (1.9) называется каноническим уравнением гиперболы. Величины а и b называются соответственно действительной и мнимой полуосями гиперболы.

6. Свойства гиперболы

1°.Гипербола имеет две оси симметрии (главные оси гиперболы) и центр симметрии (центр гиперболы). При этом одна из этих осей пересекается с гиперболой в двух точках, которые называются вершинами гиперболы. Эта ось называется действительной осью гиперболы.

Другая ось не имеет общих точек с гиперболой и поэтому называется мнимой осью гиперболы.

Таким образом, мнимая ось гиперболы разделяет плоскость на правую и левую полуплоскости, в которых расположены симметричные относительно этой оси правая и левая ветви гиперболы.

Справедливость указанного свойства симметрии гиперболы вытекает из того, что в уравнении (1.9) величины х и у фигурируют в четных степенях.

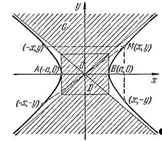
Рис. 9

Следовательно, если координаты х и у точки М удовлетворяют уравнению (1.9) (т.е. точка М располагается на гиперболе), то этому уравнению удовлетворяют координаты (-х, у) и (х,-у) симметричных ей точек относительно осей координат и координаты (-х,-у) точки, симметричной М относительно начала координат (рис. 6.6).

Таким образом, если гипербола задана своим каноническим уравнением (1.9), то главными осями этой гиперболы являются оси координат, а центром гиперболы - начало координат.

Убедимся теперь, что ось Ох является действительной осью гиперболы, точки А(-а, 0) и В (а, 0) - вершинами гиперболы и ось Оу является мнимой осью гиперболы. Для этого достаточно доказать, что ось Ох пересекает гиперболу в точках А и В, а ось Оу не имеет общих точек с гиперболой. Так как ординаты точек оси Ох равны нулю, то для выяснения величины абсцисс точек пересечения этой оси с гиперболой нужно в уравнении (1.9) положить у=0. После этого мы получим уравнение , из которого находятся абсциссы точек пересечения оси Ох с гиперболой. Полученное уравнение имеет решения х=-a и х=a. Следовательно, ось Ох пересекает гиперболу (т. е. является ее действительной осью) в точках А(-а, 0) и В (а, 0) (т. е. эти точки и есть вершины гиперболы). Поскольку абсциссы точек оси Оу равны нулю, то для ординат точек пересечения этой оси с гиперболой получаем из (1.9) уравнение , которое не имеет действительных решений. Следовательно, ось Оу является мнимой осью гиперболы.

Фокусы гиперболы располагаются на ее действительной оси.

2°. Рассмотрим область G, которая получена объединением прямоугольника D, координаты х и у точек которого удовлетворяют неравенствам |х|<а,|у|<b, и тех двух углов, образованных диагоналями этого прямоугольника, в которых располагается мнимая ось гиперболы (на рис. 6.6 эта область заштрихована). Убедимся, что в области G нет точек гиперболы.

Разобьем область G на две части G1 и G2, где G1 представляет собой полосу, абсциссы x точек которой удовлетворяют неравенству |х|<a, a G2 - остальная часть области G (Область G1 представляет собой, очевидно, полосу, заключенную между безгранично продолженными вертикальными сторонами прямоугольника D. Область G2 состоит из четырех частей, каждая из которых располагается в одном из координатных углов.)

Очевидно, в полосе G1 нет точек гиперболы, так как абсциссы х точек, расположенных на гиперболе, удовлетворяют неравенству |х| а (Из канонического уравнения гиперболы вытекает, что ). Обратимся теперь к точкам области G2. Заметим, что каждая точка G2 либо лежит на диагонали прямоугольника D, либо за его диагональю. Поскольку диагонали D определяются уравнениями и то координаты х и у точек G2 в силу их расположения удовлетворяют неравенству (Абсциссы х точек G2 не равны нулю). Из этого неравенства вытекает неравенство из которого в свою очередь следуют неравенства . а так как для точек гиперболы , то в области G2 нет точек гиперболы.

Другая информация:

Этап работы над проблемной темой
Выделите основную идею, на которую Вы будете опираться при проведении исследования; Укажите документы, постановления государства, Правительства, философские, педагогические учения, которые послужат основой исследования; Опишите научную новизну и теоретическую значимость исследования (что нового в о ...

Особенности обучения грамматике английского языкав младшем школьном возрасте
Грамматика наряду со словарным и звуковым составом представляет собой материальную основу речи. Современный токовый словарь определяет грамматику, как раздел языкознания, в котором изучаются закономерности изменения и сочетания слов, образующих осмысленные предложения или высказывания. Умение грамо ...

Диагностика психологического климата в коллективе младших школьников
Цель исследования: проверить эффективность комплекса занятий для младших школьников, разработанного на основе личностно-ориентированного подхода. Задачи исследования: 1. выявить: - особенности работы учителя начальных классов по созданию благоприятного психологического климата в коллективе младших ...