Разработка элективного курса по теме: «Кривые второго порядка»

Из последних формул вытекает, что , эти равенства означают подобие рассматриваемых парабол относительно точки О.

5°. Отметим, что кривая у2=2рх при р<0 также является параболой, которая целиком располагается в левой полуплоскости плоскости Оху. Чтобы убедиться в этом, достаточно заменить х на -х и -р на р.

9. Директрисы эллипса, гиперболы и параболы

Определение параболы, базировалось на свойстве этой кривой, которое связано с ее фокусом и директрисой. Это свойство можно сформулировать также и следующим образом: парабола есть геометрическое место точек плоскости, для которых отношение расстояния до фокуса к расстоянию до директрисы есть величина постоянная, равная единице.

Оказывается, отличный от окружности эллипс и гипербола обладают аналогичным свойством: для каждого фокуса эллипса или гиперболы можно указать такую прямую, называемую директрисой, что отношение расстояния от точек этих кривых до фокуса к расстоянию до отвечающей этому фокусу директрисы есть величина постоянная.

1. Эксцентриситет эллипса и гиперболы. Обратимся к эллипсу (гиперболе). Пусть с - половина расстояния между фокусами эллипса (гиперболы), а - большая полуось эллипса (действительная полуось гиперболы).

Определение. Эксцентриситетом эллипса (гиперболы) называется величина е, равная

e=(1.24)

Учитывая связь величины с с длинами а и b большой и малой полуосей эллипса (с длинами действительной и мнимой полуосей гиперболы) (см. формулы (1.5) и (1.10)), легко получить следующие выражения для эксцентриситета е:

для эллипса(1.25)

для гиперболы (1.25')

Из формул (1.25) и (1.25') вытекает, что эксцентриситет эллипса меньше единицы, а эксцентриситет гиперболы больше единицы

Отметим, что эксцентриситет окружности равен нулю (для окружности b= а).

Два эллипса (две гиперболы), имеющих одинаковый эксцентриситет, подобны. В самом деле, из формулы (1.25) для эксцентриситета эллипса (из формулы (1.25') для эксцентриситета гиперболы) вытекает, что эллипсы с одинаковым эксцентриситетом имеют одинаковое отношение малой и большой полуосей (гиперболы с одинаковым эксцентриситетом имеют одинаковое отношение - мнимой и действительной полуосей). Такие эллипсы (гиперболы)" подобны

Эксцентриситет эллипса можно рассматривать как меру его «вытянутости»: чем больше эксцентриситет

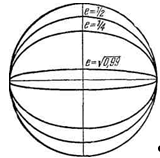
Рис. 13

е (см. формулу (1.25)), тем меньше отношение - малой полуоси эллипса b

к его большой полуоси а. На рис. 6.9 изображены эллипсы с разными эксцентриситетами, но с одинаковой большой полуосью а.

Эксцентриситет гиперболы можно рассматривать как числовую характеристику величины раствора угла между ее асимптотами. В самом деле, отношение равно

тангенсу половины угла между асимптотами гиперболы.

Директрисы эллипса и гиперболы.

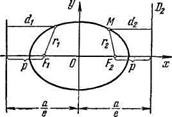
Рис. 14

1°. Директрисы эллипса. Мы выяснили, что любой, отличный от окружности, эллипс имеет большую и малую оси и центр - точку пересечения этих осей. Обозначим через с половину расстояния между фокусами F1 и F2 эллипса, через а его большую полуось и через О его центр (рис. 6.10).

Пусть е - эксцентриситет этого эллипса (так как эллипс отличен от окружности, то еО) и - плоскость, в которой расположен эллипс. Малая ось эллипса разбивает эту плоскость на две полуплоскости. Обозначим через i (i=1, 2) ту из этих полуплоскостей, в которой лежит фокус Fi (i=1, 2).

Определение. Директрисой Di (i=1, 2) эллипса, отвечающей фокусу Fi (i=1,2), называется прямая, расположенная в полуплоскости i (i = 1,2) перпендикулярно большой оси эллипса на расстоянии от его центра.

Другая информация:

Методическая служба в условиях развития республиканской системы последипломного образования педагогов
Деятельность методического кабинета улусного управления образования строилась на концептуальной идее республиканской системы последипломного образования педагогов - удовлетворять индивидуальные потребности и интересы педагогов в их профессиональном, общекультурном росте, духовном развитии. Ведущие ...

Обязательный минимум содержания образовательных программ по экономике в средней школе
Изучение экономики в школе направлено на достижение следующих целей: - освоение системы знаний, опирающихся на основы экономической науки, о структуре и логике функционирования экономики, об экономическом поведении людей, системе ценностей свободного и ответственного выбора, необходимых для взаимод ...

Методы самостоятельной работы учащихся по осмыслению и усвоению нового материала
Наряду с устным изложением изучаемого материала учителем значительное место в процессе обучения занимают методы самостоятельной работы учащихся по восприятию и осмыслению новых знаний. Это очень важные методы. К.Д. Ушинский, например, считал, что только самостоятельная работа создает условия для гл ...