Разработка элективного курса по теме: «Кривые второго порядка»

Доказательство. Убедимся, что в некоторой, специально выбранной системе координат геометрическое место точек, удовлетворяющее требованиям сформулированной теоремы, определяется при е<1 уравнением (т.e. является эллипсом), а при е>1 -уравнением (т. е. является гиперболой). Пусть R- точка пересечения прямой D и прямой А, проходящей через F перпендикулярно D (рис. 6.12). На прямой А выберем положительное направление от F к R при е<1 и от R к F при е>1 (на рис. 6.12 показан случай е<1). Так как дальнейшие рассуждения для случая е>1 и е<1 идентичны, мы проведем их подробно для е<1, т. е. для случая, определяющего эллипс. Обозначим через р расстояние между точками F и R. Вспоминая расположение директрисы эллипса относительно его центра), естественно выбрать начало О координат на прямой А слева от точки R на расстоянии. При заданных е и р величина может быть определена при помощи формулы (1.27). Иными словами, естественно положить

(1.36)

Будем теперь считать прямую А с выбранным началом О и направлением от F к R осью абсцисс. Ось ординат направим так, как указано на рис. 6.12. В выбранной системе координат фокус F имеет координаты (с, 0), где

(1.37)

а директриса D определяется уравнением

(1.38)

Перейдем теперь к выводу уравнения рассматриваемого геометрического места точек. Пусть М - точка плоскости с координатами (х, у) (рис. 6.12). Обозначим через r расстояние от точки М до фокуса F и через d расстояние от точки М до директрисы D. Соотношение ,

(1.39)

является необходимым и достаточным условием расположения точки М на геометрическом месте {М}.

Используя формулу расстояния между двумя точками М и F и формулу для расстояния от точки М до прямой D, получим

(1.40)

(1.41)

Из (1.39), (1.40) и (1.41) вытекает, что соотношение

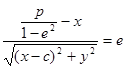(1.42)

представляет собой необходимое и достаточное условие расположения точки М с координатами х и у на геометрическом месте {М}. Поэтому соотношение (1.42) является уравнением геометрического места {М}. Путем стандартного приема «уничтожения радикалов», а также используя формулы (1.36) и (1.37), это уравнение легко привести к виду

(1.43)

где b2=а2- с2.

Для завершения доказательства нам нужно убедиться в том, что в процессе преобразования уравнения (1.42) в уравнение (1.43)не появились «лишние корни».

Убедимся в том, что расстояние r от точки М, координаты х и у которой удовлетворяют уравнению (1.43), до точки F(c,0), может быть вычислено по формуле. Используя соотношение (1.37) и формулу а = . получим для г следующее выражение:

.(1.44)

Так как точка М, координаты х и у которой удовлетворяют (1.43), расположена слева от прямой D (для таких точек х а), а для точек прямой D:,где e<1, то для расстояния d от М до D справедлива формула (1.41). Отсюда и из формулы (1.44)вытекает, что для рассматриваемых точек М выполняется соотношение , т. е. уравнение (1.43) является уравнением геометрического места . Аналогично рассматривается случай е>1.

Используя доказанную теорему и определение параболы, мы можем сформулировать следующее определение отличного от окружности эллипса, гиперболы и параболы.

Определение. Геометрическое место {М} точек М плоскости , для которых отношение е расстояния r до точки F этой плоскости к расстоянию d до прямой D, расположенной в плоскости , есть величина постоянная, представляет собой либо эллипс (при 0<е<1), либо параболу (при е=1), либо гиперболу (при е>1). Точка F называется фокусом, прямая D - директрисой, а е - эксцентриситетом геометрического места .

Другая информация:

Психофизиологические особенности развития детей младшего школьного возраста
Я. А. Коменский, выдающийся чешский педагог, был первым, кто настаивал на строгом учете в учебно-воспитательной работе возрастных особенностей детей. Он выдвинул и обосновал принцип природосообразности, согласно которому обучение и воспитание должны соответствовать возрастным этапам развития. «Всё ...

Способы организации детей на сюжетных физкультурных занятиях
Эффективность обучения физическим упражнениям обеспечивается с помощью различных способов организации детей. Эти способы при выполнении движений оказывают влияние на количество повторений за отведенное время, обеспечивают управление педагогом процессом усвоения материала, создают условия для осозна ...

Функции межпредметных связей
Межпредметные связи выполняют в обучении ряд функций. Методологическая функция выражена в том, что только на их основе возможно формирование у учащихся диалектико-материалистических взглядов на природу, современных представлений о ее целостности и развитии, поскольку межпредметные связи способствую ...