Разработка элективного курса по теме: «Кривые второго порядка»

Разумеется, время полета будет радикально сокращено, если удастся достичь скорости, сравнимой со скоростью света. Например, на разгон до половины скорости света с постоянным ускорением g~10 м/с2 (пригодной для нахождения на этом аппарате людей) будет затрачено примерно 150*106/10 = 1.5*107 c, что составит примерно полгода. Замечание о технической возможности такого режима работы двигателей остается в силе, однако если о нем пока забыть, то до ближайшей звезды (4 световых года) можно долететь примерно за 9 лет (полгода на разгон, 8 лет на свободный полет на скорости 150 тыс. км/с и еще полгода на торможение). Траекторию такого движения (кеплеровским оно уже не является) можно считать прямолинейной, поскольку ее существенное искривление возможно только на начальном этапе разгона (и конечном этапе торможения), когда аппарат будет иметь небольшую скорость и находиться сравнительно недалеко от Солнца (звезды). За все время разгона будет пройдено расстояние ~ g* = 7500 а.е. = 0.036 пк - именно на таком расстоянии от Солнца закончится фаза разгона.

4. Движение по гиперболической орбите

Для гиперболической орбиты выполняется условие V02 > .

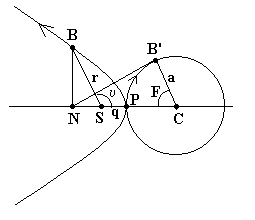
Рис. 25 - Параметры гиперболической орбиты

При рассмотрении гиперболического движения вводится особый параметр F, подобный эксцентрической аномалии у эллипса. На рис. 6 применены следующие обозначения: S - фокус гиперболы, Р - ее вершина (перицентр), C - ее центр. Положение на гиперболе произвольной точки В определяется углом между радиус-вектором SB и направлением оси апсид SP - истинной аномалией. Если из точки В опустить перпендикуляр BN на линию апсид и из точки их пересечения N провести касательную к окружности радиуса a (длина действительной полуоси гиперболы) с центром в центре гиперболы С, получим точку касания B'. Угол между радиусом этой точки и направлением на перицентр и обозначается как угол F.

Уравнение движения по гиперболе - зависимость параметра F от времени t (аналог уравнения Кеплера (7) для эллиптического движения) выглядит так:

(21)

Связь между различными параметрами эллиптической орбиты может быть выражена следующими соотношениями: (22)

(23) (24)

При t (прохождение перицентра)  = 0 и радиус-вектор достигает минимального значения rmin = q = a*(e-1), а скорость – максимального

V2max= .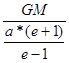

При возрастании r до бесконечности истинная аномалия увеличивается до предельного значения max = arccos(-), параметр F достигает максимального значения Fmax= 90o, а скорость - минимального значения V2min= G*.

Зависимость эксцентриситета e гиперболы от начальных радиус-вектора, скорости и угла между ними видна из формулы (14). При изменении угла от 0o до 90o e растет от 1 до emax =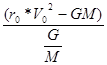, а при увеличении 0 от 90o до 180o e снова уменьшается от emax до 1. Если через а обозначить действительную ось гиперболы, то a = (25)

В предельном случае, аналогично параболе, при sin(0)=0 гипербола вырождается в полупрямую, выходящую из начала координат, которое является одновременно и вершиной, и фокусом вырожденной гиперболы.

Материал для закрепления материала по теме эллипс

Упражнения:

Упражнение 1. Докажите, что сумма расстояний от любой точки лежащей во внутренней области, ограниченной эллипсом до фокусов эллипса меньше, а от точки лежащей во внешней области эллипса больше длины большой оси.

Решение. Обозначим фокусы эллипса через F1 и F2, а точку через X. Точку пересечения луча F1X с эллипсом обозначим через Y.Пусть сначала точка X лежит во внутренней области эллипса. По неравенству треугольника F2X<XY+ +YF2, а значит, F1X +XF2 <F1X +XY + YF2 = F1Y + F2Y.(рис. 1)

Другая информация:

Методика обучения аудированию на иностранном языке на старшем этапе в средней общеобразовательной школе
На данном этапе обучения аудированию постепенно увеличивается не только длительность звучания текстов и количество незнакомых слов, но и меняется их характер. На старшем этапе обучения это уже не только рассказы, но и лекции, интервью, репортажи, выступления. Тексты для аудирования уже используются ...

Организация и проведение опытно-экспериментальной работы
Педагогический эксперимент проводился на базе МБОУ СОШ №73 г. Краснодара. В эксперименте принимали участия учащиеся 5-ых классов. В начале учебного 2012-2013 года мы начали изучение педагогических технологий, в частности здоровьесберегающих. Теоретический анализ литературных источников по теме иссл ...

Воскресные школы
Воскресная школа - занятия для детей, где в доступной, игровой форме рассказываются основы христианской веры и библейские сюжеты. Название образовано от дня проведения занятий – воскресенья. Это идея создания некой «семейной атмосферы», которая призвана не заменить ребенку его семью, а помогает реб ...