Разработка элективного курса по теме: «Кривые второго порядка»

II. способ

Приведём уравнение к каноническому виду

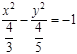, , следовательно, Строим осевой прямоугольник, а затем изображаем гиперболу.

Задачи для самостоятельного решения:

1.Найти полуоси, координаты фокусов и эксцентриситет гиперболы 9x2-16y2=36.

2. Написать каноническое уравнение гиперболы, если длина действительной оси равна 8, а расстояние между фокусами равно 10.

Материал для закрепления по теме парабола

Упражнения:

Упражнение 1:Сформулируйте и докажите утверждение, аналогичное утверждению 1 из раздела эллипс для параболы.

Решение:

Для точек лежащей во внутренней области ограниченной параболой расстояние до фокуса меньше, чем расстояние до директрисы, а для точек вне параболы наоборот (рис. 2).

Проекцию точки X на директрису обозначим через Y, а точку пересечения XY с параболой через Z. Через F обозначим фокус параболы. По определению параболы FZ = ZY. Если точка X лежит во внутренней области параболы, то XY = XZ + ZY. По неравенству треугольника FX<FZ+ZX=ZY+ZX=XY. Если точка X и парабола лежат по разные стороны от директрисы, то утверждение очевидно. Пусть точка X лежит во внешней области параболы, но по ту же сторону от директрисы, тогда ZY =ZX+XY, и по неравенству треугольника FX+XZ>FZ=ZY = =ZX+XY. А значит, FX>XY, что и требовалось доказать.

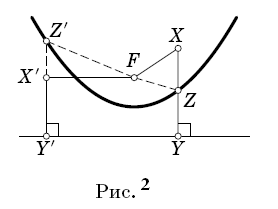
Рис. 33

Упражнение 2. Определить координаты фокуса и уравнение директрисы параболы y=x2.

Решение. Если поменять ролями оси Ох и Оу, то каноническое уравнение параболы примет вид: x2=2px. Сравнивая это уравнение с заданным, получим 2p=1, отсюда p=1/2. Следовательно, фокус параболы имеет координаты (0,1/4), а уравнение директрисы есть y=-1/4.

Упражнение 3. a) Когда достигается максимум модуля разности расстояний от точки P до точек F1 и F2, лежащих по разные стороны от прямой l ?

б) Пусть даны две прямые l и l’′ и точка F, не лежащая на них. Найдите такую точку P на прямой l, что разность расстояний от нее до прямой l′ и до точки F (взятая со знаком) максимальна.

Решение. a) Обозначим через F2′ точку, симметричную F2 относительно прямой l. Очевидно, что F2X = F2’ X для любой точки X на прямой l. Нам достаточно найти такую точку P, что разность расстояний от P до F1 и F2′

будет как можно больше. Из неравенства треугольника следует что |F1P - F2′P|<F1F2′. И достигается этот максимум тогда и только тогда, когда точки F1, F2′, P лежат на одной прямой. Поскольку точки F2 и F2′ симметричны, углы, которые образуют прямые F1P и F2P с прямой l, равны (рис. 34).

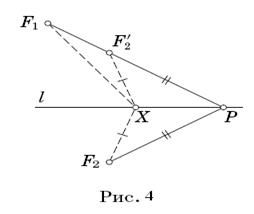
Рис. 34

б) Обозначим через F′ точку, симметричную F относительно l. Выберем ту из точек F и F′, расстояние от которой до прямой l′ минимально (расстояние берется со знаком).

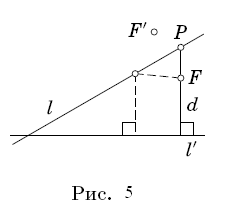
Рис. 35

Пусть это точка F. Расстояние от F до l′ обозначим через d. Тогда для любой точки P на прямой l расстояние до l′ не больше чем PF+d. А значит, требуемая в задаче разность всегда не превосходит d. С другой стороны, она равна в точности d, когда точка P лежит на перпендикуляре к l′, проведенном из точки F (рис. 5).Стоит также отметить, что если в п. а) прямая F1F2′ параллельна l, а в п. б) прямая l′ перпендикулярна l, то рассматриваемого максимума не существует (он достигается на бесконечности).

Задачи для самостоятельного решения.

1. Написать каноническое уравнение параболы, если расстояние фокуса от директрисы равно 10.

2. Определить координаты фокуса и уравнение директрисы параболы y=0.25x2.

3. Дана парабола y2=12x. Найти длину ее хорды, проходящей через точку М(8,0) и наклоненной к оси параболы под углом 60є.

4. Привести уравнение параболы x=y2-y+2 к каноническому виду и определить координаты ее вершин.

4. Зачетная работа.

Вариант 1.1. Составить каноническое уравнение эллипса по следующим данным:

a) расстояние между фокусами равно 24 и большая ось 26;b) эксцентриситет равен 0.6, расстояние между фокусами - 6.

Другая информация:

Дисциплина средневековой школы
Так как схоластическое обучение, и по составу предметов, и по языку, и по чуждым самодеятельности ученика приемам, не представляло интереса и не согласовалось с законами развивающегося, юношеского духа, то оно могло основываться только на строгой дисциплине. Вместе с тем, обучение это не могло имет ...

Цели, содержание и технология обучения диалогической реи
Основной целью обучения говорению является развитие у учащихся способности осуществлять устное речевое общение в разнообразных ситуациях. Для реализации цели необходимо развивать у учащихся навыки диалогической речи, так как в программных требованиях записано, что учащиеся должны без предварительно ...

Различные подходы к трактовке понятия функции в курсе математики в средней школе
Задача. При каких значениях параметра а уравнение имеет ровно четыре корня? Строим графики функций и в одной системе координат, воспринимая равенство как равенство значений выбранных функций. Построим график четыре точки пересечения получаем для . При (координаты точки максимума (1,2)) получаем вер ...