Разработка элективного курса по теме: «Кривые второго порядка»

Но F1Y + F2Y равно длине веревки, т. е. большой оси эллипса. Рассуждая аналогично в случае, если точка X лежит вне эллипса, получаем F2Y <XY +XF2. Следовательно, F1X+XF2 =F1Y+YX+XF2 >F1Y+F2Y.

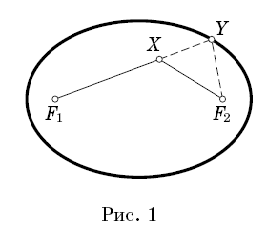
Рис. 26

Упражнение 2. Найдите геометрическое место середин хорд эллипса, параллельных данному направлению.

Решение. Рассмотрим эллипс как параллельную проекцию окружности. Тогда параллельным хордам эллипса и их серединам соответствуют параллельные хорды окружности и их середины, лежащие на диаметре окружности. Следовательно, геометрическим местом середин параллельных хорд эллипса также будет некоторый его диаметр (хорда, проходящая через центр).

Упражнение 3. С помощью циркуля и линейки найдите фокусы данного эллипса.

Решение. Построим две параллельные хорды эллипса. По предыдущему упражнению прямая, соединяющая их середины, является диаметром эллипса. Построив таким образом два диаметра, мы найдем центр эллипса О. В силу симметрии эллипса окружность с центром О пересекает эллипс в четырех точках, образующих прямоугольник со сторонами, параллельными осям эллипса. Теперь фокусы эллипса можно найти как точки пересечения большой оси и окружности с центром в конце малой оси и радиусом, равным большой полуоси.

Задачи:

Дано уравнение а) 3х2 + у2 = 7. Изобразить эллипс двумя способами.

I способ:

Запишем его в виде . Устанавливаем, что , строим осевой прямоугольник со сторонами 2R, l и изображаем сам эллипс (рис. 17). Отметим, что в правой части уравнения должно быть положительное число, а в левой – сумма квадрата абсциссы, взятого с положительным коэффициентом, и квадрата ординаты.

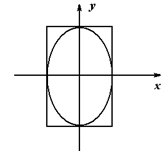
Рис. 27

II способ

Приведём уравнение к каноническому виду.

Разделим обе его части на 7.

Получим, что

Строим осевой прямоугольник со сторонами а и 2b, а затем изображаем эллипс.

Отметим, что, например, уравнение 3х2 + 5у2 = 7 следует сначала преобразовать к виду х2 + у2 = или 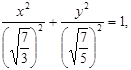а затем находить R, k и a, b соответственно.

Если центр эллипса находится не в начале координат, но его оси параллельны координатным осям, то он задаётся уравнением (4), где С (а; b) – центр эллипса. Это легко следует из формул параллельного переноса, или каноническим уравнением

(5) – С (х; у) – центр эллипса.

Данного материала достаточно для построения эллипса в том случае, если он задан уравнением, содержащем как квадраты, так и первые степени переменных.

б) Построить график

I способ

Преобразуем к виду (4):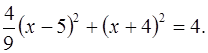

Это уравнение эллипса с центром в точке С (5; – 4), где k = 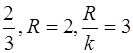(рис. 28)

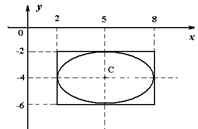
Рис. 28

II способ

Преобразуем к виду (5): . Получили уравнение эллипса с центром в точке С (5; – 4), где а = 3, b = 2.

Строим сам эллипс.

Найти длины полуосей и координаты фокусов следующих эллипсов:

а)

Приводим уравнение к каноническому виду , а = 3, b = 2.

Фокусы F1 и F2 имеют координаты F1(с; 0) и F2(– с; 0).

Итак, F1(; 0) и F2(; 0) а = 3, b = 2.

б)

Другая информация:

Интерес к рисованию и тематика рисунков
Подавляющее большинство учащихся специальной школы, особенно младших классов, любят рисовать. Дети охотно откликаются на предложение нарисовать что-нибудь и с удовольствием принимаются за работу. Для младших школьников рисование представляет своеобразную игру. Этот вид деятельности их увлекает и ра ...

Формирование обществоведческих знаний – она из задач начальной школы
Человеческое общество очень сложная и в то же время целостная система. Оно является объектом изучения многих общественных наук: философии, истории, политологии, экономики, культурологии, социологии, психологии и др. Но каждая из этих наук специализируется на изучении отдельных сторон общества и его ...

Методические рекомендации по формированию монологической речи у умственно отсталых школьников младших классов
В ходе изучения методической литературы нами были отобраны различные дидактические игры и упражнения, направленные на формирование устной монологической речи, предложенные Р.И. Лалаевой, Т.Б. Филичевой, А.В. Ястребовой, А.М. Курицыной,. Речевой и наглядный материал для данных упражнений также долже ...