Разработка элективного курса по теме: «Кривые второго порядка»

Задачи для самостоятельного решения

1. Написать каноническое уравнение эллипса, длина малой оси которого равна 6, а фокусное расстояние равно 8.

2. Написать каноническое уравнение эллипса, если известно, что расстояние между концами большой и малой оси равно 5, а сумма длин полуосей равна 7.

3. Написать каноническое уравнение эллипса, если расстояния фокуса его от концов большой оси равны 2 и 18.

Материал для закрепления теме гипербола

Упражнения:

Упражнение 1: Сформулируйте и докажите для гиперболы утверждения, аналогичные утверждению из упражнения 1из темы эллипс.

Решение.

В случае с гиперболой это утверждение формулируется следующим образом: пусть модуль разности расстояний от любой точки на гиперболе до фокусов F1 и F2 равен d. Обозначим дугу гиперболы, внутри которой лежит F1, через Г. Тогда для точек X вне Г величина XF2 −XF1 меньше d, а во внутренней области – больше. Пусть точка X лежит во внутренней области, отсекаемой дугой Г. Обозначим точку пересечения луча F2X и Г через Y. Получаем, что F2X = F2Y + YX. По неравенству треугольника F1X < F1Y + YX, значит, F2X − F1X >(F2Y+YX)−(F1Y+YX)=F2Y−F1Y=d. Если же точка X лежит вне Г, то, взяв за точку Y пересечение F1X и Г, получим F1X= F1Y + YX. По неравенству треугольника F2X<F2Y +YX. Следовательно, F2X−F1X<(F2Y+YX)−(F1Y+YX)=F2Y−F1Y=d. (рис. 31)

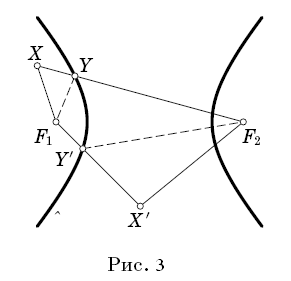
Рис. 31

Упражнение 2. Найдите геометрическое место центров окружностей, касающихся двух данных.

Решение. Рассмотрим для определенности случай, когда окружности с центрами O1, O2 и радиусами r1, r2 лежат одна вне другой. Если окружность с центром O и радиусом r касается обеих окружностей внешним образом, то OO1 =r+r1, OO2 =r+r2 и, значит, OO1 -OO2 = = r1 - r2, т. е. O лежит на одной из ветвей гиперболы с фокусами O1, O2. Аналогично если окружность касается обеих данных внутренним образом, то ее центр лежит на другой ветви этой гиперболы. Если же одно из касаний внешнее, а другое внутреннее, то модуль разности расстояний OO1 и OO2 равен r1 +r2, т. е. O описывает другую гиперболу с теми же фокусами. Аналогично если одна окружность лежит внутри другой, то искомое ГМТ состоит из двух эллипсов с фокусами O1, O2 и большими осями, равными r1 +r2 и r1 -r2. Случай пересекающихся окружностей разберите самостоятельно.

Упражнение 3. Сформулируйте и докажите оптическое свойство гиперболы.

Решение:

Сформулируем оптическое свойство для гиперболы.

Если прямая l касается гиперболы в точке P, то l является биссектрисой угла F1 PF2, где F1 и F2 – фокусы гиперболы (рис. 4).

Предположим, что биссектриса l′ угла F1PF2 пересекает гиперболу еще в какой-нибудь точке Q (лежащей на той же дуге, что и P). Для удобства будем считать, что точка P лежит на дуге, которая ближе к фокусу F1. Обозначим через F1′ точку, симметричную F1 относительно l′. Тогда F1Q=QF1′, F1 P=PF1′; кроме того, точки F2, F1′ и P лежат на одной прямой. Итак, F2P-PF1 =F2Q-F1 Q.В силу вышеуказанных равенств получаем F2 F1 =F2P − PF1 = F2 Q− QF1. Но по неравенству треугольника F2 F1 >F2 Q−QF′

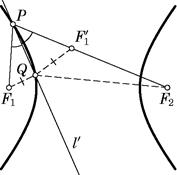
Рис. 32

Задачи:

Найти полуоси, координаты фокусов, эксцентриситет, уравнения асимптот и директрис гиперболы 9x2-16y2=144.

Решение. Приведем данное уравнение к каноническому виду (разделив его на 144):

Отсюда следует, что a2=16, b2=9. Следовательно, a=4 -действительная полуось, b=3 - мнимая полуось. Тогда Значит, фокусы имеют координаты F1(-5,0), F2(5,0). Находим эксцентриситетУравнения асимптот имеют вид , а уравнения директрис. Построить графики.

а)

I способ.

Это уравнение равносильно уравнению . Поскольку l < 0, то вершины гиперболы расположены на оси Оу. Гипербола неравнобокая, т. к. . Строим осевой прямоугольник со сторонами и , где , . Чертим график гиперболы.

Другая информация:

Использование историй с движениями при обучении грамматике английского языка в начальной школе
Одна из основных задач учителя на раннем этапе обучения детей иностранному языку – сделать этот предмет интересным. Важно учитывать в процессе обучения психологические особенности детей этого возраста. В предыдущих параграфах мы отмечали, что в младшем школьном возрасте дети эмоциональны и подвижны ...

Технология проблемного обучения
Проблемное обучение не является совершенно новой педагогической технологией. Его применяли практически на протяжении всего XX в. Это объясняется тем, что проблемность является одной из закономерностей познания, стимулирует поисковую деятельность ученика, развитие его творческого мышления. В последн ...

Григорий Богослов. Взгляд его на образование
Григорий Богослов (330—390 г.) род. в Назианзе, в Капподокии; образование получил в Александрии и Афинах. В Афинах он близко подружился с Василием Великим. Впоследствии был Константинопольским епископом, но скоро, по проискам Ариан, оставил Константинополь. Известен философским обоснованием догмата ...