Разработка элективного курса по теме: «Кривые второго порядка»
Решаем аналогично а). 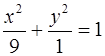 , а = 3, b = 1.
, а = 3, b = 1.
F1(с; 0), F2(– с; 0). ![]()
Итак, F1(![]() ; 0) и F2(
; 0) и F2(![]() ; 0) а = 3, b = 1.
; 0) а = 3, b = 1.
в) ![]()
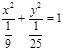 , а =
, а = ![]() , b =
, b = ![]() .
.
F1(с; 0), F2(– с; 0): ![]()
Итак, а = ![]() , b =
, b = ![]() , F1(
, F1(![]() ; 0), F2(-
; 0), F2(-![]() ; 0).
; 0).
Найти координаты точек М, принадлежащих эллипсу 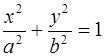 и равноудалённых от фокусов.
и равноудалённых от фокусов.
Пусть М (х; у), тогда МF1 = МF2 (по условию). Т. к. F1(с; 0), F2(– с; 0): ![]() то
то ![]()
![]()
Если х = 0, то, подставляя его в исходное уравнение, получим: ![]() ,
, ![]() Следовательно,
Следовательно, ![]() и
и ![]() .
.
Взяв на плоскости прямоугольную декартову систему координат, изобразить области, определяемые следующими системами неравенств.
а) 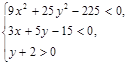
Построим множество точек, определяемых 1-м, 2-м, 3-м неравенством.
Найдём пересечение этих множеств.
Построим эллипс ![]() но т. к. неравенство строгое, то точки эллипса не принадлежат искомой области, т.е. неравенство (2) задаёт внутренние точки эллипса.
но т. к. неравенство строгое, то точки эллипса не принадлежат искомой области, т.е. неравенство (2) задаёт внутренние точки эллипса.
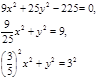
Устанавливаем, что R = 3, 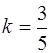 (0< k <1),
(0< k <1), 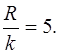 Cтроим осевой прямоугольник со сторонами
Cтроим осевой прямоугольник со сторонами 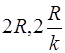 и изображаем эллипс.
и изображаем эллипс.
Строим множество точек, заданных вторым неравенством. Для этого строим прямую 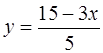 и штрихуем определяемую область.
и штрихуем определяемую область.
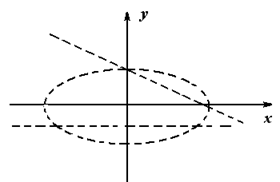
Рис. 29
Аналогичные рассуждения для построения области, заданной неравенством у + 2 > 0.
Построение.
б) 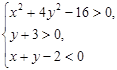
Построим множество точек, определяемых 1-м, 2-м, и 3-м неравенствами.
Найдём пересечение этих множеств.
I. ![]() – эллипс, точки которого не принадлежат искомой области (неравенство строгое), т.е. неравенство задаёт внешние точки эллипса. Приведём уравнение к каноническому виду
– эллипс, точки которого не принадлежат искомой области (неравенство строгое), т.е. неравенство задаёт внешние точки эллипса. Приведём уравнение к каноническому виду
![]()
Строим осевой прямоугольник со сторонами a и b, изображаем эллипс.
Строим множество точек, заданных неравенством (2). Для этого изображаем прямую у = 3 и штрихуем определяемую область.
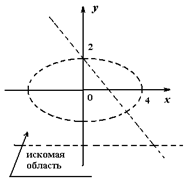
Рис. 30
Определить вид и расположение кривой ![]()
Решение. Дополним члены, содержащие х и у соответственно, до полных квадратов:
![]()
Отсюда получаем
![]()
Следовательно, кривая, заданная исходным уравнением, представляет собой эллипс с полуосями![]()
Центр эллипса находится в точке ![]() .
.
Другая информация:
Половое воспитание в семье
В число природных особенностей человека, обусловленных социальными факторами входят те, что определяются полом. Современна я наука располагает данными о том, что первые 5-6 лет жизни - это период, когда закладываются и формируются наиболее глубокие и сказывающиеся на последующем развитии слои психи ...
Гуманистический подход
Следующий подход, определяющий социокультурные основания образования, связан с его гуманизацией и гуманитаризацией. Поэтому педагогический процесс нуждается в его осмыслении с философско-этических позиций, феноменальность которых основывается на выводе о том, что XX век вошел в историю человечества ...
Экспериментальное исследование грамматического строя речи у дошкольников с
общим недоразвитием речи III уровня
Логопедическое обследование направлено на выявление у детей сформированности грамматического строя речи. В возрасте, когда процесс развития речи далеко не завершен, специалисту необходимо разграничивать, что уже должно быть сформировано в детской речи, что только начинает складываться, и каких лекс ...
Разделы
- Главная
- Семейное воспитание
- История педагогических систем
- Межпредметные связи в обучении
- Программированное обучение
- Основы коррекционной педагогики
- Культура речи и профессионализм
- Материалы о педагогике
