Разработка элективного курса по теме: «Кривые второго порядка»

При этом не исключается совпадение фокусов эллипса. Очевидно, если фокусы совпадают, то эллипс представляет собой окружность.

Для вывода канонического уравнения эллипса выберем начало О декартовой системы координат в середине отрезка F1F2, а оси Ох и Оу направим так, как указано на рис. 6 (если фокусы F1 и F2 совпадают, то О совпадает с F1 и F2, а за ось Ох можно взять любую ось, проходящую через О).

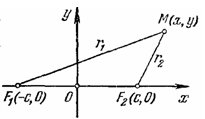
Рис. 6

Пусть длина отрезка F1 F2 равна 2с. Тогда в выбранной системе координат точки F1 и F2 соответственно имеют координаты (-с, 0) и (с, 0). Обозначим через 2а постоянную, о которой говорится в определении эллипса. Очевидно, 2а>2с, т. е. a>с (Если М - точка эллипса (см. рис. 6.2), то |MF1| + |MF2| = 2a, а так как сумма двух сторон MF1 и MF2 треугольника MF1F2 больше третьей стороны F1F2=2c, то 2а>2с.) Случай 2а=2с естественно исключить, так как тогда точка М располагается на отрезке F1F2 и эллипс вырождается в отрезок.). Пусть М - точка плоскости с координатами (х, у) (рис. 6.2). Обозначим через r1 и r2 расстояния от точки М до точек F1 и F2 соответственно. Согласно определению эллипса равенство

r1+r2=2а(1.1)

является необходимым и достаточным условием расположения точки М (х, у) на данном эллипсе.

Используя формулу расстояния между двумя точками получим

(1.2)

Из (6.1) и (6.2) вытекает, что соотношение

(1.3)

представляет собой необходимое и достаточное условие расположения точки М с координатами х и у на данном эллипсе. Поэтому соотношение (1.3) можно рассматривать как уравнение эллипса. Путем стандартного приема «уничтожения радикалов» это уравнение приводится к виду

(1.4)

Где b2=a2-c2(1.5)

Так как уравнение (1.4) представляет собой алгебраическое следствие уравнения эллипса (1.3), то координаты х и у любой точки М эллипса будут удовлетворять и уравнению (1.4). Поскольку при алгебраических преобразованиях, связанных с избавлением от радикалов, могли появиться «лишние корни», мы должны убедиться в том, что любая точка М, координаты которой удовлетворяют уравнению (1.4), располагается на данном эллипсе. Для этого, очевидно, достаточно доказать, что величины r1 и r2 для каждой точки удовлетворяют соотношению (1.1). Итак, пусть координаты х и у точки М удовлетворяют уравнению (1.4). Подставляя значение у2 из (1.4) в правую часть выражения (1.2) для r1 после несложных преобразований найдем, что

. Так как а + > 0,то r1 = а +.

Совершенно аналогично найдем, что r2= а -.

Таким образом, для рассматриваемой точки М

r1= а+, r2= а - (1.6)

т. е. r1+r2=2a, и поэтому точка М располагается на эллипсе. Уравнение (1.4) называется каноническим уравнением эллипса. Величины а и Ь называются соответственно большой и малой полуосями эллипса (наименование «большая» и «малая» объясняется тем, что а>b). Если полуоси эллипса а и b равны, то эллипс представляет собой окружность, радиус которой равен R=a=b, а центр совпадает с началом координат.

4. Свойства эллипса

1°. Эллипс имеет две взаимно перпендикулярные оси симметрии (главные оси эллипса) и центр симметрии (центр эллипса). Действительно, в уравнении (1.4) величины х и у фигурируют в четных степенях. Следовательно, если координаты х и у точки М удовлетворяют уравнению (1.4) (т.е. точка М располагается на эллипсе), то этому уравнению удовлетворяют координаты (-х, у) и (х, -у) симметричных ей точек относительно осей координат и координаты (-х, -у) точки, симметричной М относительно начала координат (рис. 7).

Таким образом, если эллипс задан своим каноническим уравнением (1.4), то главными осями этого эллипса являются оси координат, а центром эллипса - начало координат. Точки пересечения эллипса с главными осями называются вершинами эллипса. Точки А, В, С, D на рис. 7 - вершины эллипса. Очевидно, эти вершины имеют соответственно координаты

Другая информация:

Характеристика показателей нормального психического развития ребенка раннего возраста
Существуют определенные поведенческие ориентиры, позволяющие заподозрить нарушение темпа психического развития ребенка. Знание этих ориентиров полезно и необходимо тем, кто несет ответственность за воспитание ребенка. Итак: К 1 году – ребенок использует 7-14 слов, сосредоточенно занимается одним де ...

Как помочь ребёнку в обучении
Поступление в школу – поистине переломный момент в жизни ребёнка. Резко изменяется весь образ его жизни, в условиях, в которых он действует; он обретает новое положение в обществе; у него складываются совершенно иные взаимоотношений с взрослыми и сверстниками. Ведущей деятельностью, становится учеб ...

Диагностика уровня математического развития детей младшего школьного возраста
Для проведения экспериментальной работы нами были выбраны 2 «А» и 2 «Б» классы, из которых и сформированы две подгруппы – экспериментальная и контрольная – по 8 человек с приблизительно одинаковым уровнем развития математических представлений. Вначале была проведена диагностика уровня развития дете ...