Опорные задачи по теме «Многогранники»

3.

Сколько нужно взять прямоугольников и ка­ким свойством они должны обладать, чтобы из них можно было составить прямоугольный параллеле­пипед?

Решение. Два прямоугольника для оснований со сторонами а и b, четыре прямоугольника для боковой грани. Из них два со сторонами с и а и два со сторонами с и b.

4

. Установите, прямой или наклонной является призма, у которой две смежные боковые грани пер­пендикулярны основанию.

Решение. Призма является прямой. Две смеж­ные боковые грани пересекаются по прямой, пер­пендикулярной плоскости основания. Остальные ребра параллельны данному ребру и, следователь­но, тоже перпендикулярны основанию.

5.

Исследуйте, существует ли призма, имеющая 50 ребер? 54 ребра?

Решение. Число ребер n-угольной призмы 3n, поэтому призмы, имеющей 50 ребер, не существу­ет, а 54 ребра имеет 18-угольная призма.

6.

Какой многоугольник лежит в основании призмы, если она имеет n граней?

Решение. Число сторон многоугольника, ле­жащего в основании, равно числу боковых граней призмы. Из условия следует, что это число равно n - 2, так как в призме две грани являются основа­ниями. Таким образом, в основании (n - 2)-уголь­ник.

3)Задачи на доказательство.

1.

В параллелепипеде диагонали основания рав­ны, а боковое ребро перпендикулярно двум смеж­ным сторонам основания. Докажите, что паралле­лепипед прямоугольный.

Доказательство. В основании - параллелограмм с равными диагоналями, т.е. прямоугольник, а бо­ковое ребро перпендикулярно основанию по при­знаку перпендикулярности прямой и плоскости.

2.

Докажите, что число ребер призмы кратно 3.

Доказательство. В n-угольной призме боковых ребер n, а ребер нижнего и верхнего оснований 2n, всего 3n ребер.

3.

Докажите, что сумма двугранных углов при всех боковых ребрах четырехугольной призмы рав­на 360".

Доказательство. Рассмотрим перпендикулярное сечение призмы. В сечении - четырехугольник, сумма его углов S = 180°(4 - 2) = 360°.

4.

Если призма имеет 18 граней, то в ее основа­нии лежит 16-угольник. Докажите.

Доказательство. У призмы две грани оснований и, значит, боковых граней 16. Следовательно, в основании 16-угольник.

5

. В кубе из вершины N проведены диагонали граней NE, NF, NK Концы их соединены отрез­ками (рис. 4.7). Докажите, что многогранник NEFK­ - правильный тетраэдр.

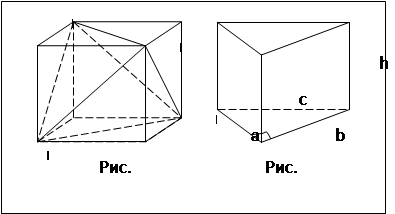6.

Если две боковые грани треугольной призмы взаимно перпендикулярны, то сумма квадратов их площадей равна квадрату площади третьей боко­вой грани (рис. 4.8). Докажите.

7.

Докажите, что сечение параллелепипеда пло­скостью не может быть правильным пятиугольни­ком.

Доказательство. Среди сторон многоугольника в сечении параллелепипеда плоскостью найдутся параллельные, а у правильного пятиугольника ни­какие две стороны не параллельны.

4)Задачи на построение

Сечения можно рисовать на заранее подготов­ленном изображении призмы.

1.

Постройте сечение куба в виде: а) треугольни­ка, б) четырехугольника, в) пятиугольника, г) ше­стиугольника.

2

. Постройте плоскость, проходящую через сто­рону нижнего основания треугольной призмы. Ка­кие многоугольники получаются в сечении приз­мы при вращении этой плоскости вокруг стороны?

Ответ: сечение может иметь форму

треугольника, трапеции.

3.

В правильной треугольной призме плоскость сечения ВСМ образует с плоскостью основания двугранный угол α (рис. 4.9). Постройте линейный угол этого двугранного угла. Дайте объяснения.

Построение. Проведем из вершины A правиль­ного треугольника АВС высоту АК. Точка K принадлежит ребру ВС. Соответственно отрезок МК перпендикулярен ребру ВС. Угол МКА­ - искомый.

4.

В основании прямой призмы (рис. 4.10) лежит равнобедренная трапеция. Сечение ABC1D1 обра­зует с плоскостью основания двугранный угол α. Постройте его линейный угол.

Другая информация:

Деятельность социального педагога в приемной семье
Одной из наиболее оптимальных форм замещающего семейного воспитания можно считать передачу ребенка на опеку в приемную семью. Опека и попечительство являются общими технологиями социальной работы, применимы при оказании помощи разным категориям населения и, прежде всего, используются для защиты пра ...

Характеристика психофизиологического состояния учащихся с нарушением интеллектуального развития старшего возраста
Под умственной отсталостью следует понимать стойкое необ­ратимое нарушение познавательной деятельности, возникшее в результате органического поражения головного мозга. В данном определении четко выделяются два взаимосвязан­ных диагностических критерия: психолого-педагогический (стой­кое нарушение п ...

Инновационные технологии в системе образования: опыт и перспективы
В современных условиях общество ставит перед образованием задачу предоставить каждому человеку свободный открытый доступ к образованию на протяжении всей жизни с учетом собственных интересов, способностей и потребностей, обеспечив при этом приспособляемость к жизни в условиях высокой скорости инфор ...