Разработка формы учебных и методических материалов для учителя по теме "Линейная функция"

Задания на отработку (номера из учебника А.Г. Мордковича, которые соответствуют содержанию этапа).

Форму предъявления контрольно-оценочных заданий учащимся учитель выбирает самостоятельно. Например, они могут быть даны как задания проверочной работы или как индивидуальные задания для учащихся.

Таблица №1 дает общее представление об этапах логики введения понятия, тогда как таблица №2 позволяет раскрыть содержание этапов более подробно.

Результаты анализа текстов УМК программы А.Г. Мордковича, показывают, что в курсе много внимания уделяется свойствам функций, но не элементам, составляющим это понятие. Для выявления того, в какой степени у школьников, обучающихся по разным программам, сформировалось представление о функции как об однозначной зависимости (однозначном соответствии между переменными), необходимо подобрать диагностический материал.

В 2003 году нами было проведено пилотное исследование сформированности понятия функция в 9 классе. Целью этого исследования было опробовать диагностические задания на предмет того, в какой степени учащиеся могут работать с провокационными утверждениями, могут ли они различать два вида зависимостей.

Учащиеся выбранного нами класса, начиная с 7 класса, обучались по программе А.Г. Мордковича. Нами был выбран 9 класс, поскольку уже пройдены этапы наглядно-интуитивного и рабочего уровней использования понятия функции, темы, в которых рассматриваются примеры неоднозначных зависимостей, сформулировано общее определение функции. Авторами предполагается, что к концу 9 класса у учащихся основные характеристики понятия сформированы.

Задания содержали материал, который знаком учащимся и соответствует их уровню знаний. Задания были выписаны на доску учителем, носили статус безоценочной, диагностической работы. Возможность использовать учебник и другие средства, задавать вопросы не оговаривалась. Учащиеся вопросов при выполнении работы не задавали, учебники не использовали. На выполнение заданий потребовалось 20 минут.

Диагностика №1

Задание №1. Пусть y=f(x)

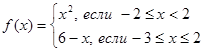
1. Найдите f(-3), f(-2), f(1), f(2) используя график или формулу;

2.Изобразите множество точек (x, f(x));

3.Найдите наибольшее и наименьшее значение y=f(x);

4.Является ли y=f(x) функцией?

Цель задания – проверить смогут ли учащиеся, опираясь на свой опыт и анализируя данные, полученные в ходе выполнения задания, выявить неоднозначный характер предложенной зависимости.

В задании №1 задана кусочная зависимость, представленная системой двух функций, которая сама функцией не является, поскольку есть промежуток, на котором однозначность нарушается. В первом пункте задания значения независимой переменной подобраны так, что при подстановке их в формулы, или используя график, учащиеся бы получили два значения зависимой переменной. Учащиеся должны были найти значения зависимой переменной при заданных значениях независимой переменной, построить график зависимости, по которому возможно было бы увидеть неоднозначность. Нами предполагалось, что учащиеся при ответе на вопрос №4 обратят внимание на данные, которые получили при построении графика и при поиске значений зависимой переменной, и смогут сделать вывод, является ли предложенная зависимость функциональной. Наибольшее и наименьшее значение предлагается найти для того, чтобы проверить степень владения одним из свойств функций. Структура задания предполагает, что учащиеся умеют делать вывод на основании результатов выполненных действий, имеют некоторый опыт работы с контрпримерами.

Задание №2

Определение. Числовой функцией с областью определения D называется соответствие, при котором каждому числу х из множества D сопоставляется по некоторому правилу единственное число у, зависящее от х.

Вопрос. Какие из следующих формул можно назвать функциями?

х=׀у׀b) c) y=2

Цель задания – выявить смогут ли учащиеся, опираясь на предложенное определение числовой функции, определить те формулы, которые задают не однозначное соответствие между переменными. Мы предполагали, что учащиеся прочитают определение, выделят в качестве существенного аспекта понятия числовой функции, опираясь на этот факт и свой опыт работы с функциями смогут ответить на вопрос задания.

Нами были получены следующие результаты.

В первом задании график кусочной "функции" был построен верно практически всеми учениками , причем кусок прямой ребята строили с помощью "двух точек", а параболу "по памяти". При выполнении п.1 все учащиеся предпочли находить значения "функции" в заданных точках используя аналитическое задание. Значения в заданных точках многие учащиеся находили используя только одну из формул, некоторые не выполнили это задание, а остальные определили верно по два значения в предложенных точках, но подозрений у них это не вызвало. Только один человек из класса определил, что предложенная зависимость не функциональная.

Другая информация:

Внеклассная деятельность как одна из форм работы
Вопросу внеурочной деятельности посвятили свои исследования такие авторы, как В. О. Кутьев, В. Д. Шадриков, И. Д. Демакова и др. Так, В. О. Кутьев в своей работе "Внеурочная деятельность школьников" отмечает, что "внеурочная деятельность - это такая организация труда, познания и обще ...

Лекция
Итак, лекция (от лат. lectio – чтение) – систематическое, последовательное, монологическое изложение преподавателем (лектором) учебного материала, как правило, теоретического характера; главное звено дидактического цикла обучения. Является традиционной формой для высшей школы, где на её основе форм ...

Система оказания специализированной помощи детям с ограниченными возможностями здоровья в России
Законом РФ «Об образовании лиц с ограниченными возможностями здоровья (специальном образовании)» предусмотрено получение образования детьми, имеющими специальные образовательные потребности в форме обычного обучения в общеобразовательных учреждениях, интегрированного обучения, обучения на дому и об ...