Введение понятия функции в программе А.Г. Мордковича "Алгебра 7"

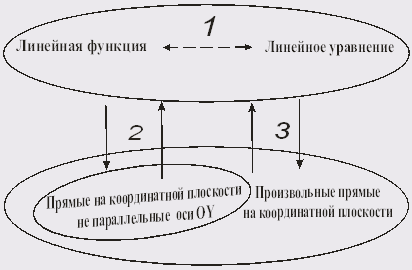
График линейной функции – это "способ представления зависимости, который позволяет для каждого значения х просто увидеть готовое значение у без всяких вычислений" . График выступает в качестве геометрической модели зависимости, тогда как формула – алгебраическая модель. В курсе представлен переход от одного вида моделей к другому. Поскольку авторы говорят о неоднозначных зависимостях, то линейными функциями можно описать любые прямые, непараллельные оси ОY. На основании этого переход ГЛФ ↔ЛФ восстанавливаются однозначно.

Таким образом схема анализа способа введения понятия функции в курсе С.Ф. Горбова изображена на рис.1.3.

Историческая реконструкция понятия функции, проведенная в §1 настоящей главы, позволила выделить этапы его развития: 1) этап становления понятия функции как зависимости рядов величин, а затем переменных; 2) разделение однозначных и неоднозначных зависимостей; 3) введение понятия области определения. При этом важную роль играл вопрос о соотнесении геометрического образа и аналитической формы задания функции.

В ходе восстановления логики программы мы выделили два объекта для введения понятия линейной функции: линейное уравнение с двумя неизвестными и его график. Логика изложения представлена четырьмя блоками: раскрытие связи линейного уравнения и его графика; оформление связи линейной функции с ее геометрической моделью; введение области определения функции и рассмотрение нового способа построения прямой. Последние два блока не имеют логических связок с предыдущими. Автор рассматривает функцию как частный случай уравнения, при этом, не раскрывая представление о функции как зависимости между переменными. Мы попытались установить логические связи между геометрическими и аналитическими интерпретациями линейной функций и линейного уравнения, и увидели, что связи не являются полными. Это приводит к математическим неточностям, например, к тому, что прямая у=с не является графиком линейной функции. Другие виды функций получаются путем обобщения формы записи линейной функции.

В программе МАРО понятие функции построено в соответствии с его историческим развитием, что позволяет авторам работать с отношением между аналитической и геометрической формами задания. Связи между понятиями линейное уравнение, линейная функция и их графики восстанавливаются практически полностью, отсутствуют лишь явные переходы между алгебраическими формами задания линейной функции и линейного уравнения. В данном курсе авторы работают с понятием зависимости вообще, с любыми видами функций, рассматриваются также и неоднозначные зависимости. В силу этого линейная функция представлена лишь как частный случай однозначной зависимости.

Другая информация:

Музыкальное мышление: многоуровневость исследования
Мышление (англ. – thinking; немец. – denkens; франц. – pensee), в общем виде, определяется как процесс обобщённого отражения действительности, возникший из чувственного познания на основе практической деятельности человека. Будучи сложным социально-историческим феноменом, мышление изучается многими ...

Урок музыки и экологическое воспитание школьников
В современной педагогической науке эстетическое воспитание школьников средствами музыкального искусства трактуется неоднозначно. С одной стороны утверждается значимость эстетического воспитания в становлении общей духовной картины внутреннего мира каждого школьника как личности. С другой — некоторы ...

Основные принципы андрагогики
Основное положение андрагогики, в отличие от традиционной педагогики, заключается в том, что ведущую роль в процессе обучения играет не обучающий, а обучаемый. Функцией обучающего в этом случае является оказание помощи обучающемуся в выявлении, систематизации, формализации личного опыта последнего, ...