Подходы к определению выпуклого многогранника

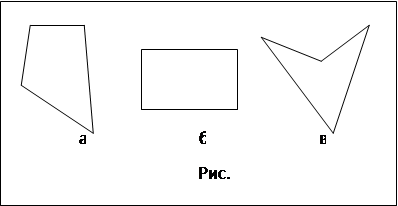После введения понятия многогранника в школе, как правило, рассматривают выпуклые многогранники. Удачным считается подход, когда сразу дается определение выпуклого многогранника и для него определяются элементы, что сделать легче. Изучение свойств как выпуклых многоуголь­ников, так и выпуклых многогранников занимает очень большое место в школьном курсе геомет­рии. Однако точный смысл понятия «вы­пуклый» в средней школе не раскрывается и причины, заставляющие требовать вы­пуклости рассматриваемых многоугольни­ков и многогранников, нигде не объясняют­ся. Учащиеся часто вообще не воспринима­ют смысла прилагательного «выпуклый» и лишь по привычке, машинально в ответ на предложение изобразить какой-либо че­тырехугольник рисуют фигуру, изображен­ную на рисунке l.4,а (а иногда даже фигуру, изображенную на рис 1.4,б), а не фигу­ру, изображенную на рис l.4,в. При этом может показаться, что лишь недостаток об­щей математической культуры заставляет их считать все четырехугольники выпуклы­ми, подобно тому как наиболее слабые школьники иногда не в состоянии предста­вить себе четырехугольника, отличного от прямоугольника (рис.

1.4,б), параллело­грамма или, в лучшем случае, от трапеции. В некоторых случаях игнорирование усло­вия о выпуклости многоугольника или мно­гогранника оказывается даже совершенно законным - какую, например, ценность имеет оговорка о выпуклости в теореме: сумма углов выпуклого n-угольника равна (n - 2) .180° Условие этой теоремы пол­ностью сохраняет силу и для невыпуклых (простых) многоугольников; так, например, ясно, что сумма углов и невыпуклого четы­рехугольника (рис. 1.4,в) равна 360°. Прав­да, приводимое в школе доказательство теоремы справедливо лишь для выпук­лых многоугольников.

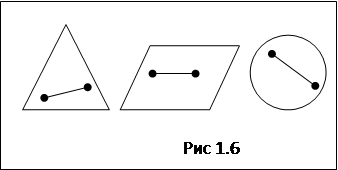
Понятие выпуклого многогранника чаще всего вводят по аналогии с выпуклым многоугольником. Очень хорошо эта аналогия просматривается в учебнике Александрова. Существует два способа определения выпуклого многогранника. Многогранник называется выпуклым, если он лежит по одну сторону от каждой из ограничивающих его плоскостей. Такой подход принят в учебниках. Либо многогранник называется выпуклым, если любые две его точки могут быть соединены отрезком. Такое определение дается в учебнике. В учебнике за основу берется второе определение и доказывается возможность другого (в нашем случае первого) определения.

Остановимся подробнее на втором определении. Чаще всего в геометрии рассматривают связные фигу­ры, т. е. такие, в которых любые две точки можно соединить линией, целиком принад­лежащей этой фигуре. При этом соединяю­щая линия может оказаться довольно слож­ной (рис 1.5). Естественно выделить класс фигур, для которых в качестве линии, со­единяющей две ее точки А, В, всегда мож­но выбрать самую простую линию - прямо­линейный отрезок АВ. Такие фигуры на­зываются выпуклыми.

Фигура F называется вы­пуклой, если вместе с каждыми двумя точ­ками А, В она целиком содержит и весь отрезок АВ. Примеры выпуклых фигур показаны на рис.1.6; на рис. 1.7 изображены неко­торые невыпуклые фигуры.

Кроме плоских, можно рассматривать пространственные выпуклые фигуры (их обычно называют выпуклыми телами). Примерами могут служить тетраэдр, параллелепипед, шар, шаровой слой и другие.

Другая информация:

Организация экспериментального исследования по рассматриваемой проблеме
При разработке методики констатирующего эксперимента основополагающим является современное понимание психологического и психофизиологического содержание процесса письма в норме. Осуществлялась опора на результаты исследований, касающихся этиологии, патогенеза, симптоматики структуры дефекта при общ ...

Коррекционно-педагогическая работа по формированию навыков самообслуживания у детей дошкольного возраста с нарушением интеллекта
Главное для детей с умственной отсталостью – это максимально овладеть навыками самообслуживания, научиться ориентироваться в окружающем мире самостоятельно, насколько это возможно. Поэтому педагогам, родителям и другим специалистам необходимо выбирать наиболее оптимальные условия и формы обучения и ...

Современные задачи и содержание уроков чтения в старших классах специальной школы 8 вида
На уроках чтения в 7 - 9 классах продолжается формирование у школьников техники чтения: правильности, беглости, выразитель­ности на основе понимания читаемого материала. Это связано с тем, что не все учащиеся старших классов в достаточной степени владе­ют указанными навыками. Кроме того, изучение к ...