Логико-историческая реконструкция понятия функции

Понятие функции как зависимость между величинами

Отношение между постоянными величинами

Представители ранней математики искали отношения между величинами, а не числами, но как результаты измерения величин получали ряды чисел.

Одним из примеров существования зависимости в Древней Греции является отношение золотого сечения. Деятели Древней Греции большое внимание уделяли эстетическому аспекту своих творений, которые должны были удовлетворять принципу соизмеримости основным пропорциям человека. Одним из таких отношений является отношение золотого сечения, которое фиксирует прежде всего пропорции между основными частями тела человека. Задачу о золотом сечении можно сформулировать так: "Найти такой способ разделить целое на две части – меньшую и большую, чтобы была верна пропорция: меньшая часть относится к большей так же, как большая к целому". Задачу нахождения величин, удовлетворяющих соотношению, решали в древнегреческую эпоху исходя из геометрических рассуждений, при этом использовался "словесный", описательный способ передачи сведений, ныне применяется алгебраический аппарат.

Итак, можно заметить, что изначально рассматривались ряды, составленные из чисел, полученных при измерении постоянных величин, связанных между собой определенным отношением.

Отношение переменных величин

Физические переменные величины отличаются от постоянных тем, что они изменяются под воздействием внешних факторов, например, с течением времени.

Одним из первых, кто рассмотрел отношение между переменными величинами, был Кеплер. Он решал следующую астрономическую задачу: известно расстояние, которая прошла планета за конкретный месяц, необходимо определить какое расстояние она пройдет за следующий месяц. Он сделал допущение, что для правильного расчета положения планет и звезд в заданный момент времени можно использовать конические сечения. Так, по Кеплеру планеты движутся вокруг Солнца по эллиптическим орбитам. Теперь требовалось научно предсказать положение точки на кривой в любой момент времени. Кеплер сформулировал задачу на математическом языке, что позволило использовать соответствующий аппарат. На математическом языке задача формулируется следующим образом: "Известны ряды величин х и у, существует зависимость между ними, необходимо найти форму описания этой зависимости, которая была бы проста, помогала упростить вычисления, выполненные на основе геометрических соображений". Для решения задачи он разбил эллипс на сектора, близкие, по свойствам к секторам окружности. Так Кеплер свел вычисления для эллипса к задачи о движении тела по окружности, т.е. решал следующую задачу: "Математически описать путь, пройденный точкой по прямой или окружности, находящийся в постоянном отношении ко времени". Таким образом, появилась секториальная скорость, как отношение изменения расстояния, пройденного планетой, за определенный промежуток времени. На современном математическом языке формулу секториальной скорости можно записать так: ω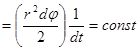 где dφ – изменение величины угла сектора окружности радиуса r, dt –изменение времени. Поскольку описание формулы площади сектора окружности было известно , то появилась возможность обозначить площадь сектора эллипса Sсек.эл.=ω(φ)d(φ). Так появился первый случай рассмотрения переменного (величина угла изменяется с течением времени) внутри задачи отношения величин (отношение величины расстояния к величине времени).

Другая информация:

Отечественный опыт профильного обучения
Российская школа накопила немалый опыт по дифференцированному обучению учащихся. Каким же был опыт дифференциации общего среднего образования в дореволюционной России? Первая попытка осуществления дифференциации обучения в школе относится к 1864 г. Соответствующий Указ предусматривал организацию се ...

Методика проведения подвижных игр
Первым условием успешного использования подвижных игр в воспитании детей является знание программных задач, определенных для конкретной возрастной группы, с которой работает воспитатель. Усвоив общие задачи воспитания, необходимо применять их с учетом индивидуальных особенностей каждого ребенка. Дл ...

Методика организации лабораторно-практической работы
Учебная педагогическая практика организуется в рамках учебного процесса, согласно учебного плана по специальности «Технология и предпринимательство», и направлена на практическое освоение студентами различных видов педагогической деятельности. Главное содержание учебной педагогической практики сост ...