Изучение многогранников в школьном курсе математики

В школьных учебниках после изучения «бес­конечно-протяженных» и в силу этого весьма абстрактных геомет­рических фигур: прямых и плоскостей (вернее сказать, их взаимного расположения в пространстве) изучаются зримые, «конечные», даже, можно сказать, осязаемые пространственные фигуры, и в пер­вую очередь многогранники. Многогранник {точнее, модель много­гранника) можно изготовить, повертеть в руках, «развернуть» его поверхность или даже «разрезать» - посмотреть на сечение. В дан­ной теме это весьма существенно, и учителю необходимо использо­вать значительно расширившиеся возможности привлечения наглядности, наглядных средств (не забывая уделять достаточное внима­ние и построению проекционных чертежей). О наглядных средствах поговорим немного позднее.

Можно указать на такие две проводимые методологические линии в изучении геометрии многогранников: это их классификация и изу­чение различного рода количественных характеристик. Конечно, эти линии переплетаются между собой. В данной теме рассматри­ваются простые характеристики - численные: длины ребер, высоты, величины углов, площади поверхностей, - и качественные, типа «правильности». Собственно говоря, качественные характеристики - ­это одна из основ классификации многогранников. Если исключить стоящие чуть в стороне от ведущей линии курса правильные много­гранники (пять «платоновых тел»), то логическую схему классификации «школьных» многогранников можно описать примерно следующим образом. Рассматриваются (и строго опреде­ляются) только два вида многогранников: призмы и пирамиды. Конечно, внутри этих видов проводится грубая классификация по числу углов - призмы и пирамиды бывают n-угольными, где n = 3, 4, 5,… . Более детальная классификация - по взаимному располо­жению ребер и граней, по виду граней. Для призм она относительно «разветвленная»:

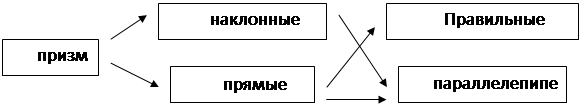
И далее:

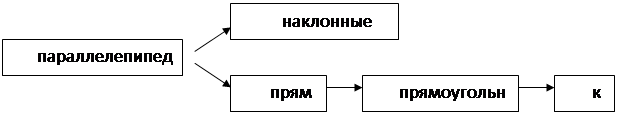
Школьная классификация пирамид менее разветвленная:

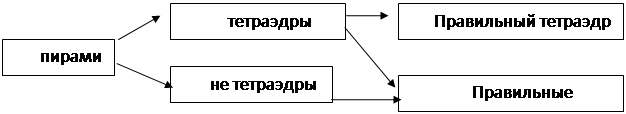
Первая задача учителя - добиться от всех учащихся знания этой классификации в том виде, в каком она подается в учебном пособии, т. е. в виде соответствующих определений. И у ученика, и у учителя при изучении данной темы может возникнуть вполне естествен­ный вопрос: почему столько внимания (и столько задач) посвящается всего лишь трем частным типам многогранников - параллелепипе­дам, правильным призмам и правильным пирамидам? Причин по крайней мере три: 1) эти многогранники нужны для дальнейшего построения теории (главным образом теории объемов); 2) они обладают симметрией, как многие формы природы и творения рук человеческих (скажем, архитектурные формы); 3) они обладают «хорошими свойствами», т. е. для них можно сформулировать и доказать достаточно простые теоремы.

Последнее преимущество обусловлено свойствами симметрично­сти; с другой стороны, как раз «хорошие свойства» и используются в теоретических целях. Все теоремы этой темы относятся к «избран­ным» многогранникам, причем совсем просто доказываются и на­половину имеют вычислительный характер (т. е. вид формул). По­этому вторая задача учителя - добиться знания учащимися всех теорем (с доказательствами).

Третья по счету, но первоочередная для учителя задача - на­учить школьников решать задачи. Практически все задачи (упраж­нения) темы вычислительные, большую часть из них составляют простые или совсем простые задачи, и здесь перед учителем рас­крываются большие возможности в продолжение линии обучения школьников эвристическим приемам решения задач. В задачах на­ходят отражение и главные методологические идеи решения задач - аналогия стереометрии с планиметрией, све­дение стереометрических задач к планиметрическим.

Другая информация:

Причина педагогического конфликта и его особенности
Взаимодействие учителя с учениками организуется через разрешение педагогических ситуаций. По Н.В. Кузьминой педагогическая ситуация – это «реальная обстановка в учебной группе и в сложной системе отношения и взаимоотношения учащихся, которую нужно учитывать при принятии решения и способах воздейств ...

Умственная отсталость как форма нарушения интеллекта:классификация, виды и причины формирования
Понятие «умственная отсталость» (олигофрения) в отечественной специальной психологии понимается как стойкое нарушение познавательной деятельности, возникшее вследствие органического поражения головного мозга (наследуемого или приобретённого). Согласно современным научным представлениям, понятие «ум ...

Категории «технология», «педагогическая технология», «технология обучения»
Сегодня в педагогической и психологической литературе часто встречается понятие «технология». Легко установить, что означает слово «технология», образованное от латинских слов «технос» - искусство, мастерство, ремесло и «логос» - наука. Технологией обычно называют процесс переработки исходного мате ...