Методическая схема изучения функций. Изучение функций в классе функций

.

Пользуясь таким представлением, найти разность функций

и

в точках .

c) Вычислить значение функции при , пользуясь таблицами Брадиса (или компьютером).

Наводящий вопрос : каким из двух способов вычисления значений данного выражения проще провести выкладки?

Целесообразно при изучении графиков функций рассмотреть графическую иллюстрацию функций вида

, ,

используя построения по точкам и учитывая простейшие особенности тех функций, которые составляют формулу данной функции.

Изучение операций второй группы вводятся посредством явного определения. Каждая из этих операций используется в изучении теоретического материала: композиция функций – сложная функция.

Понятие обратной функции, можно отнести к числу важнейших общих понятий в составе функциональной линии. При изучении выясняется зависимость её монотонности от монотонности её исходной функции.

Понятие непрерывности используется при построении графиков и способствует формированию понятия. Понятие непрерывности используется при изучении квадратного корня, при определении показательной функции, при рассмотрении графического метода решение уравнений и неравенств.

При изучении функций в X-XI классах большее предпочтение отдаётся аналитическому исследованию, и схема изучения функции выглядит следующим образом:

1) Рассмотреть подводящую задачу;

2) Сформулировать определение функции;

3) Провести аналитическое исследование свойств функции;

4) Построить (на основе данных аналитического исследования) график функции; в целях более точного его построения составить таблицу " характерных" значений функции и построить соответствующие графики;

5) Рассмотреть задачи и упражнения на применение изученных свойств функции.

Знакомя учащихся со свойствами функции, следует помнить, что не все из них являются достаточно наглядными, поэтому не всегда график функции может подсказать их ученику. Например, посмотрите на рисунок

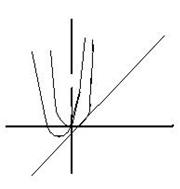
Графики каких функций здесь изображены?

Графики: и сумма функций .

Наиболее характерные случаи срабатывания "наглядности графиков":

1. корни уравнения

2. решение

Другая информация:

Основы педагогического взаимодействия с родителями школьника
Важным звеном в построении воспитательной работы является взаимодействие педагога с родителями школьника. Семья – та естественная среда жизни и развития ребенка, в которой закладываются основы личности. Какую бы сторону развития ребенка мы не взяли, всегда окажется, что решающую роль на том или ино ...

Система оказания специализированной помощи детям с ограниченными возможностями здоровья в России
Законом РФ «Об образовании лиц с ограниченными возможностями здоровья (специальном образовании)» предусмотрено получение образования детьми, имеющими специальные образовательные потребности в форме обычного обучения в общеобразовательных учреждениях, интегрированного обучения, обучения на дому и об ...

Принципы построения современных систем непрерывного образования на основе интернет-технологий
Современное состояние общества таково, что персонал практически любого предприятия должен постоянно повышать свою компетентность. Таким образом должен реализовываться принцип «образование – через всю жизнь». Очевидно, что занятое население не всегда имеет возможность физически присутствовать в учеб ...