Сравнительный анализ учебников по геометрии для 10-11-х классов

В процессе написания работы была проанализирована литература по геометрии с целью выявления способа введения материала в 10-11-х классах по данной теме.

такие кривые как парабола и гипербола отдельно не рассматриваются, а эллипс вводится через задачу, в которой учащимся предстоит выяснить, в какую фигуру В учебнике геометрии за 11 класс автора И.М. Смирнова (гуманитарный профиль)переходит окружность при параллельном проектировании.

«Пример Выяснить, какая фигура является параллельной проекцией окружности.

Решение. Пусть F - окружность в пространстве, F' - ее проекция на плоскость к в направлении прямой I. Если прямая I параллельна плоскости окружности или лежит в ней, то проекцией окружности является отрезок, равный диаметру окружности. Рассмотрим случай, когда прямая I пересекает плоскость окружности.

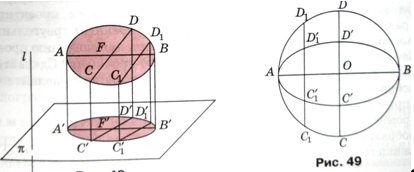
Рис. 2

Пусть AB - диаметр окружности, параллельный плоскости его проекции на эту плоскость. Тогда АВ = А'В'. Возьмем какой, другой диаметр CD и пусть C’D’ - его проекция. Обозначим отношение С’D’: CD через k. Так как при параллельном проектировании сохраняются параллельность и отношение длин параллельных отрезков, то для произвольной хорды C1D1, параллельной диаметру CD, ее проекция С1’D1’ параллельна C’D’ и отношение C1’D1’: C1D1 будет равно k.

Таким образом, проекция окружности получается сжатием или растяжением окружности в направлении какого-нибудь ее диаметра в то же число раз. Такая фигура на плоскости называется эллипсом».

В учебнике по геометрии для 10-11-х классов (профильный уровень) наряду с введением эллипса как и в гуманитарном, предусмотрено расширение курса, в котором рассматриваются кривые: гипербола, парабола и эллипс более подробно. Рассмотрим способ введения каждой из них.

Первой рассматривается парабола, как геометрическое место точек. Далее представлен способ построение с помощью линейки, угольника и нити. Вводится определение оси параболы, как прямая, проходящая через фокус и перпендикулярная директрисе, вводится определение касательной, и доказывается теорема.

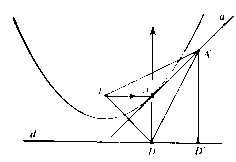
Рис. 3

«Пусть А - точка на параболе с фокусом F и директрисой d, AD - перпендикуляр, опущенный на директрису (рис 343). Тогда касательной к параболе, проходящей через точку А, будет прямая, содержащая биссектрису угла FAD».

На основе этой теореме вводится фокальное свойство параболы и рассматривается задача о построении касательной к параболы. В конце материала по параболе предусмотрена небольшая лабораторная работа, в которой учащимся предлагается получить параболу из листа бумаги.

Далее авторы вводят эллипс, также как и парабола, эллипс вводится как геометрическое место точек. Дается определение фокуса и способ построение эллипса с помощью нитки и карандаша. Далее вводится определение касательной к эллипсу, как прямой имеющей одну общую точку с эллипсом, и точку касания, как общую точку и доказывается теорема:

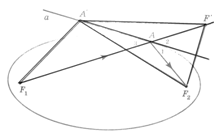
Рис. 4

«Пусть А - произвольная точка эллипса с фокусами F1,F2. Тогда касательной к эллипсу, проходящей через точку А, является прямая, содержащая биссектрису угла, смежного с углом F1AF2.»

Далее авторы вводят фокальное свойство эллипса, и рассматривается задача о построении касательной к эллипсу, решить которую предлагается с помощью циркуля и линейки. И в завершении дается лабораторная работа, в которой предлагается учащимся сделать эллипс из листа бумаги.

Другая информация:

Развитие пространственного мышления в изучении геометрического материала
В младшем школьном возрасте происходит интенсивное развитие психологических процессов: восприятия, памяти, узнавания, воображения, мышления. Геометрический материал в гораздо более высокой степени, чем арифметический, и алгебраический, соответствует ведущему в младшем школьном возрасте виду мышлени ...

Музыка как средство всестороннего развития детей
Традиционно музыка рассматривается как фактор эмоционального, творческого, эстетического и нравственного развития детей. Менее изучен аспект, связанный с воспитанием их умственной активности. Теоретические предпосылки данной проблемы прослеживаются в трудах философов Аристотеля, Демокрита, Пифагора ...

Пути и приемы реализации МПС на уроках технологии
В ХХI веке происходят качественные изменения в сфере общественного производства: техническая революция перерастает в технологическую. Технологически образовывать ученика значит в интересах, прежде всего его собственных, а также общества, государства сформировать у него жизненно важные общетрудовые ...