Подготовка и реализация уроков геометрии с использованием ИКТ

-развивающая: развить способность анализировать и актуализировать полученные знания;

-воспитательная: воспитать аккуратность, эстетическое восприятие окружающего мира.

Методы: объяснительно-иллюстративный.

Оборудование: компьютер, мультимедийный проектор, интерактивная доска, раздаточный материал.

Структура урока:

1.Организационный момент (1 мин.)

2.Объяснение новой темы (15 мин.)

3.Закрепление.(25 мин.)

4.Подведение итогов(4 мин.)

Ход урока.

Учитель: Напомните мне ребята определение треугольника.

Учитель: Ваше первое задание: разместите элементы треугольника. Давайте вспомним названия всех элементов треугольника (сторона, вершина, угол – учитель убирает шторку, на словах задан эффект множественного клонирования).

Учитель: Вот теперь их можно расставить (у доски работает 1 ученик).

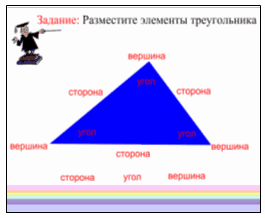
Учитель: Молодцы ребята. Что общего у этих геометрических фигур на следующей странице?

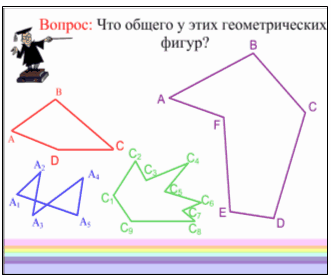
Учитель: Рассмотрим фигуру, составленную из отрезков AB, BC, CD, …, EF, FA так, что смежные отрезки (т. е. АВ и ВС, ВС и СD, …, EF и АВ) не лежат на одной прямой, а несмежные отрезки не имеют общих точек. Такая фигура называется многоугольником (рисунок на ИД). Точки А, В, С .Е, Г называются вершинами, а отрезки АВ, ВС, ., ЕF, FА — сторонами многоугольника. Сумма длин всех сторон называется периметром многоугольника.

Многоугольник с п вершинами называется п-угольником; он имеет п сторон. Примером многоугольника является треугольник. На рисунке изображены четырехугольник АВСD и шестиугольник АВСDEF. Фигура зелёного цвета, изображенная на этом рисунке не является многоугольником, так как несмежные отрезки А1А5 и А2А3 (а также А3А4 и А1А5) имеют общую точку.

Две вершины многоугольника, принадлежащие одной стороне, называются соседними. Отрезок, соединяющий любые две не соседние вершины, называется диагональю многоугольника.

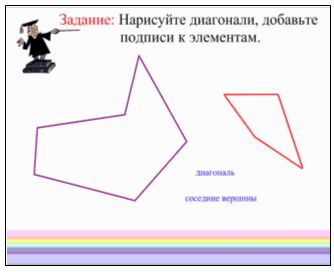
Учитель: Следующее задание. Подпишите все элементы многоугольников. Нарисуйте диагонали (на слова диагональ и соседние вершины задан эффект множественного клонирования).

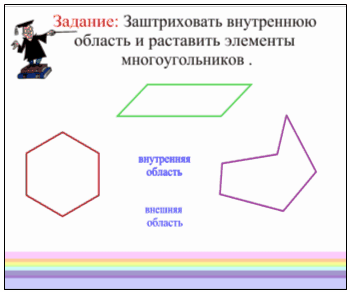
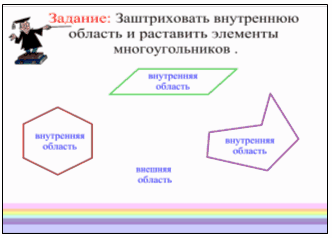
Учитель: Любой многоугольник разделяет плоскость на две части, одна из которых называется внутренней, а другая — внешней областью многоугольника. На рисунке внутренние области многоугольников заштрихованы. Фигуру, состоящую из многоугольника и его внутренней области, также называют многоугольником. Наше новое задание: давайте заштрихуем все внутренние области многоугольников. А затем обозначим новые элементы многоугольника (Слова внизу экрана БЕЗ эффекта множественного клонирования, однако слова «внутренняя область» - это 3 наложенных друг на друга словосочетания, ровно для трёх областей, а слова «внешняя область» - только в одном экземпляре). После правильного расположения вид такой:

Учитель: Многоугольник называется выпуклым, если он лежит по одну сторону от каждой прямой, проходящей через две его соседние вершины. Как вы думаете, ребята, правильно ли я расставила новые определения? Почему нет?

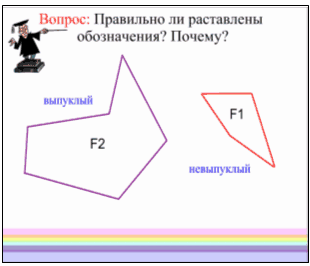
Учитель: Давайте проверим правильность вашего ответа опытным путем: проведём прямые линии через все соседние вершины обоих многоугольников (у доски 1 ученик маркером рисует прямые).

Другая информация:

Планирование межпредметных связей
Содержание, объем, время и способы использования знаний из других предметов можно определить только на основе планирования. Для этого необходимо тщательное изучение рекомендаций, данных учебными программами в разделах «Межпредметные связи» по каждой учебной теме курса, а также изучение учебных план ...

Психолого-педагогическая характеристика учащихся начальных классов специальных школ
Умственно отсталые дети - одна из наиболее многочисленных категорий детей, отклоняющихся в своем развитии от нормы. Они составляют около 2,5% от общей детской популяции. Понятие «умственно отсталый ребенок» включает весьма разнообразную по составу массу детей, которых объединяет наличие повреждения ...

Экспериментальное обучение на основе использования историй с движениями при обучении грамматики английского языка в начальной школе
На основе теоретических положений было проведено экспериментальное обучение, целью которого было выявление эффективности использования историй с движениями для формирования грамматических навыков по теме Present Simple в начальной школе. Экспериментальная работа проводилась на базе средней общеобра ...