Подходы к определению многогранника

Данная теорема позволяет определить многогранник как фигуру, составленную из тетраэдров так, что выполнены условия.

Такое определение, которое характеризует предмет тем способом, каким он может быть построен, называется конструктивным. Полученное определение многогранника именно такое; любой многогранник строится последовательным прикладыванием тетраэдров по граням; а как строить тетраэдры – известно.

В противоположность этому определения многогранника, рассмотренные ранее, состоят в указании его характерных свойств или, иначе говоря, в точном его описании. Такие определения называют дескриптивными, т.е. описательными.

Описательное определение многогранника позволяет судить о фигуре, является ли она многогранником или нет. Посмотрел со всех сторон на данное тело, увидел, что всюду его поверхность состоит из многоугольников, - значит, многогранник. Такой же характер имеют, например, обычные определения призмы и пирамиды.

Как и для многогранника, конструктивные определения можно дать многоугольникам многогранной поверхности.

4)

Другой подход к определению многогранника представлен в книге В.Г. Болтянского «Элементарная геометрия», построенный на основе вейлевской векторной аксиоматики геометрии. Этот подход не применяется в школьных учебниках, но для примера можно привести одно из определений.

При вейлевском изложении геометрии первоначальными понятиями являются точка, вектор и следующие операции над ними: паре точек сопоставляется некоторый вектор, сумма векторов, произведение вектора на число и скалярное произведение, а также их свойства.

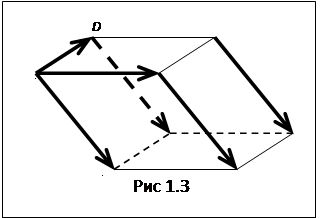Наиболее известным примером многогранника является параллелепипед. Его можно описать следующим образом. Берется параллелограмм ABCD и из его вершин откладываются равные векто­ры АА1=ВВ1 =СС1 =DD1 =e, где с не параллелен плоскости параллелограмма ABCD

(рис. 1.3).

Определение частных видов многогранников (призмы, пирамиды и др.) в данном подходе практически не отличаются от определений в школьном курсе, однако интересен сам подход к определению на основе другой аксиоматике.

Таким образом, определение многогранника может быть дано различными способами, и в разной литературе и в разных учебниках можно встретить различные подходы к определению.

Можно дать понятию многогранника как дескриптивное, так и конструктивное определение, как определение, основанное на наглядном представлении, так и строгое. Можно определить многогранник как тело и как поверхность. Различны также определения многогранника, данные на основе различных аксиоматик. В школьных учебниках чаще дается какое-то одно определение, но полезно учащимся показывать и другие способы определения многогранника.

Как и при введении понятия многогранника, существуют различные способы введения выпуклых многогранников и правильных многогранников. Рассмотрим эти способы подробнее.

Другая информация:

Методические рекомендации по формированию монологической речи у умственно отсталых школьников младших классов
В ходе изучения методической литературы нами были отобраны различные дидактические игры и упражнения, направленные на формирование устной монологической речи, предложенные Р.И. Лалаевой, Т.Б. Филичевой, А.В. Ястребовой, А.М. Курицыной,. Речевой и наглядный материал для данных упражнений также долже ...

Практическое применение методов активизации самостоятельной работы учащихся на уроках иностранного языка
Использование современных методов обучения является основой при организации самостоятельной работы учащихся на уроке. Одним из таких методов можно считать проблемный метод обучения. Он получил своё распространение в 20-30-х гг. 20в. в советской и зарубежной школе. Он основывается на теоретических п ...

Гуманистические принципы отбора содержания и методов реализации дизайнобразования старшеклассников
Всесторонний подход к анализу предмета исследования в рамках нашей квалификационной работы позволил выявить основные принципы осуществления дизайнобразования на гуманистических основах. Этим принципам отнесены: личностно-деятельностный, личностно-развивающий, принцип научности, ценностной ориентаци ...