Различные подходы к трактовке понятия функции в курсе математики в средней школе

Задача. При каких значениях параметра а уравнение имеет ровно четыре корня?

Строим графики функций и в одной системе координат, воспринимая равенство как равенство значений выбранных функций.

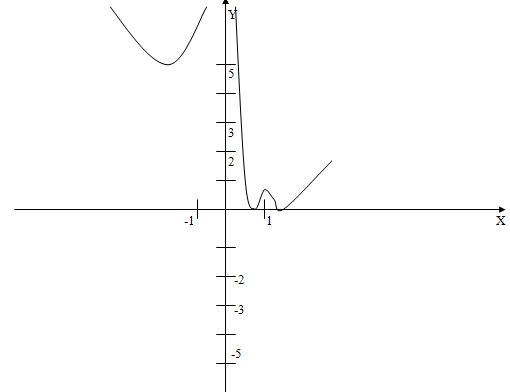
Построим график четыре точки пересечения получаем для . При (координаты точки максимума (1,2)) получаем верхнее ограничение. Второй промежуток значений для : от точки минимума функции, т.е. . Основа решения – использование функциональных и графических представлений, а само решение – переход от исследования данного в уравнении к исследованию функции. При построении графика этой функции с помощью элементарных преобразований графиков наиболее трудным является оценивание значения выражения . В качестве подсказки можно воспользоваться неравенством:

Показанный метод называется функционально-графическим моделированием. Освоение его и с формальной, и с прикладной стороны в значительной мере подчинено изучение всей функциональной линии курсов алгебры и начала анализа.

Различают две основные математические трактовки понятия функции:

1) генетическую;

2) логическую.

Основные понятия, используемые при генетической трактовке: переменная величина, функциональная зависимость переменных величин, формула (выражающая одну переменную через некоторую комбинацию других переменных), декартова система координат на плоскости. Достоинство такого подхода состоит в том, подчеркивая динамический характер понятия функциональной зависимости, выявляется модельный аспект понятия функции относительно изучения явлений природы. Например, общая схема применения функции для описания результатов опыта имеет вид:

1)провести эксперимент;

2)составить по результатам эксперимента таблицу значений связанных друг с другом величин;

3)построить по табличным данным график;

4)подобрать эмпирическим путём формулу для данной функции;

5)дать развёрнутую характеристику свойств функции;

6)истолковать установленные свойства функции на языке эксперимента.

Однако ограничительная черта в этом подходе в том, что переменная всегда неявно предполагается пробегающей непрерывный ряд числовых значений. Поэтому понятие связывается с числовыми функциями числовог8о аргумента.

Логическая трактовка: обучение функциональным представлениям следует строить на основе методического анализа понятия функции в поисках понятия алгебраической системы. Здесь функция – отношение специального вида между двумя множествами, удовлетворяющее условие функциональности. Начальный этап изучения – понятие отношения. Реализация логического подхода вызывает необходимость иллюстрировать понятие функции при помощи разнообразных средств: формулы, таблицы, задание функции стрелками, перечислением пар, использованием не только числового, но и геометрического материала(теперь и геометрическое преобразование можно рассматривать как функцию). Однако наработанные таким образом общие понятия в дальнейшем связываются только с числовыми функциями одного числового аргумента, поэтому при таком подходе наблюдается определённая избыточность в формировании функции как обобщённого понятия.

Другая информация:

Роль учителя в организации межпредметных связей
Обучение - двусторонний процесс. Даже искусственно ограничив его лишь информационной стороной, можно показать, что деятельность учителя и ученика неодинаковы. Учитель преподает учащимся знания, выявляет логические связи между отдельными частями содержания, показывает возможности использования этих ...

Содержание и современные требования к организации контроля
В условиях большей самостоятельности, при делегировании многих прав и полномочий самой школе, а значит, и повышения ее ответственности контрольно-диагностическая функция внутришкольного управления должна занять особое место в целях стимулирования деятельности учителя и ученика. Сочетание администра ...

Особенности школьного экономического образования в профильном обучении
Потребность в профессиональном самоопределении – одна из ведущих потребностей, она выступает как фактор развития личности. Одно из средств удовлетворения этой потребности в современной школе – дифференцированное обучение. В XX в. российская школа накопила немалый опыт в этой области. Достаточно пер ...